Question

16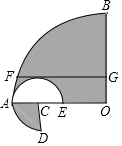．如图，扇形AOB与扇形DCE的圆心角分别为90°和270°，扇形DCE的弧过点A，FG∥AO，且与扇形DCE的弧相切，点F，G分别在弧AB，半径OB上，FG=2cm，则图中阴影部分的面积为πcm²．

Answer 1

分析 连接OF，由平行线的性质得到∠FCO=90°，根据勾股定理得到CF²=OF²-OC²=4，根据切线的性质得到CH⊥CF，推出四边形CHGO是矩形，由矩形的性质得到OG=CH=AC，根据扇形的面积公式即可得到结论．

解答 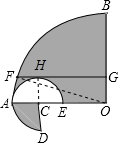解：连接OF，
∵FG∥AO，∠AOB=90°，
∴∠FCO=90°，
∴CF²=OF²-OC²=4，
设FG与⊙C相切于H，连接CH，
则CH⊥CF，
∴四边形CHGO是矩形，
∴OG=CH=AC，
∵扇形DCE的圆心角为270°，
∵∠ACE=180°，
∴∠ACD=90°，
∴S_半圆ACE=2S_扇形ACD，
∴阴影部分的面积=S_扇形AOB-S_扇形ACD=$\frac{90π•O{F}^{2}}{360}$-$\frac{90π•O{G}^{2}}{360}$=$\frac{90π•（O{F}^{2}-O{G}^{2}）}{360}$=$\frac{90π×4}{360}$=πcm²．
故答案为：π．

点评 本题考查了切线的性质，扇形面积的计算，勾股定理，平行线的性质，是基础知识比较简单．