题目内容
8.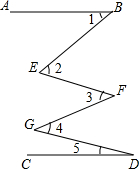 如图,已知AB∥CD,试说明∠1+∠3+∠5=∠2+∠4.
如图,已知AB∥CD,试说明∠1+∠3+∠5=∠2+∠4.
分析 过E作EM∥AB,过F作FN∥AB,过G作GQ∥AB,求出AB∥EM∥FN∥GQ∥CD,根据平行线的性质得出∠1=∠BEM,∠EFN=∠FEM,∠GFN=∠FGQ,∠5=∠DGQ,即可得出答案.
解答 解:过E作EM∥AB,过F作FN∥AB,过G作GQ∥AB,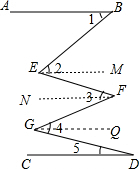
∵AB∥CD,
∴AB∥EM∥FN∥GQ∥CD,
∴∠1=∠BEM,∠EFN=∠FEM,∠GFN=∠FGQ,∠5=∠DGQ,
∴∠1+∠EFN+∠GFN+∠5=∠BEM+∠FEM+∠FGQ+∠DGQ,
∴∠1+∠EFG+∠5=∠BEF+∠FGD,
即∠1+∠3+∠5=∠2+∠4.
点评 本题考查了平行线的判定和性质的应用,能正确运用定理进行推理是解此题的关键,注意:平行线的判定有:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行,反之亦然.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知正方形的边长为a,面积为S,则( )
| A. | a=$\sqrt{S}$ | B. | a=$\sqrt{S}$ | C. | S=$\sqrt{a}$ | D. | S=±$\sqrt{a}$ |
18.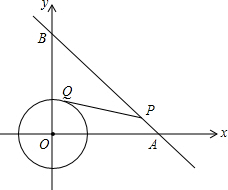 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )| A. | 3 | B. | 4$\sqrt{2}$ | C. | 6-$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
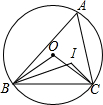 如图,△ABC的内心为I,∠A=52°,则∠BIC=116°,O为△ABC的外心,则∠BOC=100°.
如图,△ABC的内心为I,∠A=52°,则∠BIC=116°,O为△ABC的外心,则∠BOC=100°.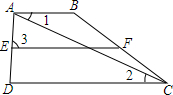 如图所示,已知AB∥EF,∠1=∠2,试说明∠3=∠D.
如图所示,已知AB∥EF,∠1=∠2,试说明∠3=∠D.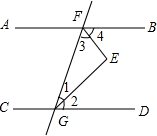 如图,∠1=∠2,∠3=∠4,且∠2+∠3=90°,试说明AB∥CD.
如图,∠1=∠2,∠3=∠4,且∠2+∠3=90°,试说明AB∥CD.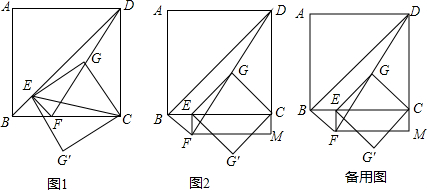
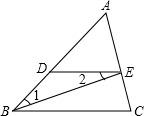 如图,BE平分∠ABC,且∠1=∠2,DE与BC平行吗?说明你的理由.
如图,BE平分∠ABC,且∠1=∠2,DE与BC平行吗?说明你的理由.