题目内容
【问题探究】
(1)如图①,点E是正△ABC高AD上的一定点,请在AB上找一点F,使EF=
AE,并说明理由;
(2)如图②,点M是边长为2的正△ABC高AD上的一动点,求
AM+MC的最小值;
【问题解决】
(3)如图③,A、B两地相距600km,AC是笔直地沿东西方向向两边延伸的一条铁路.点B到AC的最短距离为360km.今计划在铁路线AC上修一个中转站M,再在BM间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由A到M再通过公路由M到B的总运费达到最小值,请确定中转站M的位置,并求出AM的长.(结果保留根号)

(1)如图①,点E是正△ABC高AD上的一定点,请在AB上找一点F,使EF=
| 1 |
| 2 |
(2)如图②,点M是边长为2的正△ABC高AD上的一动点,求
| 1 |
| 2 |
【问题解决】
(3)如图③,A、B两地相距600km,AC是笔直地沿东西方向向两边延伸的一条铁路.点B到AC的最短距离为360km.今计划在铁路线AC上修一个中转站M,再在BM间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由A到M再通过公路由M到B的总运费达到最小值,请确定中转站M的位置,并求出AM的长.(结果保留根号)

考点:作图—应用与设计作图
专题:
分析:(1)根据等边三角形的性质得出∠BAD=30°,得出EF=
AE;
(2)根据题意得出C,M,N在一条直线上时,此时
AM+MC最小,进而求出即可;
(3)作BD⊥AC,垂足为点D,在AC异于点B的一侧作∠CAN=30°,作BF⊥AN,垂足为点F,交AC于点M,点M即为所求,在Rt△ABD中,求出AD的长,在Rt△MBD中,得出MD的长,即可得出答案.
| 1 |
| 2 |
(2)根据题意得出C,M,N在一条直线上时,此时
| 1 |
| 2 |
(3)作BD⊥AC,垂足为点D,在AC异于点B的一侧作∠CAN=30°,作BF⊥AN,垂足为点F,交AC于点M,点M即为所求,在Rt△ABD中,求出AD的长,在Rt△MBD中,得出MD的长,即可得出答案.
解答:解:(1)如图①,作EF⊥AB,垂足为点F,点F即为所求.
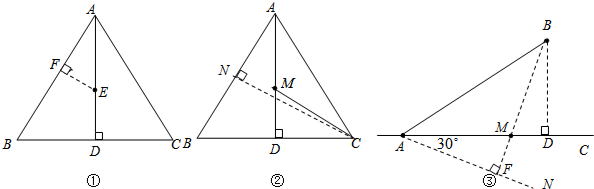
理由如下:∵点E是正△ABC高AD上的一定点,
∴∠BAD=30°,
∵EF⊥AB,
∴EF=
AE;
(2)如图②,作CN⊥AB,垂足为点N,交AD于点M,此时
AM+MC最小,最小为CN的长.
∵△ABC是边长为2的正△ABC,
∴CN=BC•sin60°=2×
=
,
∴MN+CM=
AM+MC=
,
即
AM+MC的最小值为
.
(3)如图③,作BD⊥AC,垂足为点D,在AC异于点B的一侧作∠CAN=30°,
作BF⊥AN,垂足为点F,交AC于点M,点M即为所求.
在Rt△ABD中,AD=
=
=480(km),
在Rt△MBD中,∠MBD=∠MAF=30°,得MD=BD•tan30°=120
(km),
所以AM=(480-120
)km.

理由如下:∵点E是正△ABC高AD上的一定点,
∴∠BAD=30°,
∵EF⊥AB,
∴EF=
| 1 |
| 2 |
(2)如图②,作CN⊥AB,垂足为点N,交AD于点M,此时
| 1 |
| 2 |
∵△ABC是边长为2的正△ABC,
∴CN=BC•sin60°=2×
| ||
| 2 |
| 3 |
∴MN+CM=
| 1 |
| 2 |
| 3 |
即
| 1 |
| 2 |
| 3 |
(3)如图③,作BD⊥AC,垂足为点D,在AC异于点B的一侧作∠CAN=30°,
作BF⊥AN,垂足为点F,交AC于点M,点M即为所求.
在Rt△ABD中,AD=
| AB2-BD2 |
| 6002-3602 |
在Rt△MBD中,∠MBD=∠MAF=30°,得MD=BD•tan30°=120
| 3 |
所以AM=(480-120
| 3 |
点评:此题主要考查了正三角形的性质以及锐角三角函数关系和勾股定理等知识,利用特殊角的三角函数关系得出是解题关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图,在一张长方形纸片ABCD中,AB=3
如图,在一张长方形纸片ABCD中,AB=3 已知,如图B、D、A在一直线上,且∠D=∠E,∠ABE=∠D+∠E,BC是∠ABE的平分线,求证:DE∥BC.
已知,如图B、D、A在一直线上,且∠D=∠E,∠ABE=∠D+∠E,BC是∠ABE的平分线,求证:DE∥BC.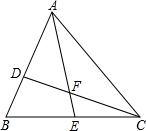 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1-S2的值为
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1-S2的值为