题目内容
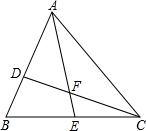 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1-S2的值为
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADF的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1-S2的值为考点:三角形的面积
专题:
分析:S△ADF-S△CEF=S△ABE-S△BCD,所以求出△ABE的面积和△BCD的面积即可,因为AD=2BD,BE=CE,且S△ABC=12,就可以求出△ABE的面积和△BCD的面积.
解答:解:∵BE=CE,
∴BE=
BC,
∵S△ABC=12,
∴S△ABE=
S△ABC=
×12=6.
∵AD=2BD,S△ABC=12,
∴S△BCD=
S△ABC=4,
∵S△ABE-S△BCD=(S△ADF+S四边形BEFD)-(S△CEF+S四边形BEFD)=S△ADF-S△CEF,
即S△ADF-S△CEF=S△ABE-S△BCD=6-4=2.
故答案为2.
∴BE=
| 1 |
| 2 |
∵S△ABC=12,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=2BD,S△ABC=12,
∴S△BCD=
| 1 |
| 3 |
∵S△ABE-S△BCD=(S△ADF+S四边形BEFD)-(S△CEF+S四边形BEFD)=S△ADF-S△CEF,
即S△ADF-S△CEF=S△ABE-S△BCD=6-4=2.
故答案为2.
点评:本题考查三角形的面积,关键知道当高相等时,面积等于底边的比,根据此可求出三角形的面积,然后求出差.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠P=60°,则∠AEB=
如图,PA、PB分别切⊙O于点A、B,点E是⊙O上一点,且∠P=60°,则∠AEB= 如图,AB为⊙O的直径,C是
如图,AB为⊙O的直径,C是
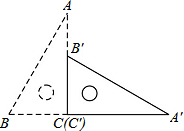 如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为
如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为