题目内容
(1)甲、乙、丙三只不透明的口袋中都装有1个白球、1个红球,它们除颜色外都相同,搅匀后分别从三只口袋中任意摸出1个球,求从三只口袋摸出的都是红球的概率.
(2)甲、乙、丙、丁四位同学分别站在正方形场地的四个顶点A、B、C、D处,每个人都以相同的速度沿着正方形的边同时出发随机走向相邻的顶点处,那么甲、乙、丙、丁四位同学互不相遇的概率是 .
①
;②
;③
;④
.
(2)甲、乙、丙、丁四位同学分别站在正方形场地的四个顶点A、B、C、D处,每个人都以相同的速度沿着正方形的边同时出发随机走向相邻的顶点处,那么甲、乙、丙、丁四位同学互不相遇的概率是
①
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
考点:列表法与树状图法
专题:
分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与从三只口袋摸出的都是红球的情况,再利用概率公式即可求得答案;
(2)由乘法公式可得共有2×2×2×2×2=16(种)等可能的结果,其中甲、乙、丙、丁四位同学互不相遇的有2种情况,然后利用概率公式求解即可求得答案.
(2)由乘法公式可得共有2×2×2×2×2=16(种)等可能的结果,其中甲、乙、丙、丁四位同学互不相遇的有2种情况,然后利用概率公式求解即可求得答案.
解答:解:(1)画树状图得:

∵共有8种等可能结果,从三只口袋摸出的都是红球的1种情况,
∴从三只口袋摸出的都是红球的概率是
.
(2)∵甲、乙、丙、丁四位同学分别站在正方形场地的四个顶点A、B、C、D处,每个人都以相同的速度沿着正方形的边同时出发随机走向相邻的顶点处,共有2×2×2×2×2=16(种)等可能的结果,其中甲、乙、丙、丁四位同学互不相遇的有2种情况,
∴甲、乙、丙、丁四位同学互不相遇的概率是:
=
.
故答案为:③.

∵共有8种等可能结果,从三只口袋摸出的都是红球的1种情况,
∴从三只口袋摸出的都是红球的概率是
| 1 |
| 8 |
(2)∵甲、乙、丙、丁四位同学分别站在正方形场地的四个顶点A、B、C、D处,每个人都以相同的速度沿着正方形的边同时出发随机走向相邻的顶点处,共有2×2×2×2×2=16(种)等可能的结果,其中甲、乙、丙、丁四位同学互不相遇的有2种情况,
∴甲、乙、丙、丁四位同学互不相遇的概率是:
| 2 |
| 16 |
| 1 |
| 8 |
故答案为:③.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点(6,-8)是直角坐标系中的一点,O为坐标原点,则OA的长度为( )
| A、6 | B、8 | C、10 | D、12 |

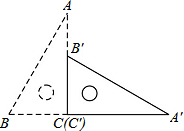 如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为
如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为 如图,在△ABC中,∠C=90°,∠ABC=15°,DE垂直平分AB,BD=3,则DC=
如图,在△ABC中,∠C=90°,∠ABC=15°,DE垂直平分AB,BD=3,则DC=