题目内容
某水果批发商计划购买某种水果,在甲果园用2000元将这种水果的可摘果全部定购却仍然不够,还需已定购水果数量的一半,于是批发商又用了1100元在相邻的乙果园购进所需水果.只是单价比在甲果园购买的要贵0.1元/千克.
(1)这种水果批发商一共购买了多少千克?
(2)该批发商将货物运回邻市批发销售.已知在运输途中水果有15%的损耗,运费为820元,为使获得的利润不低于2200元,该批发商的批发价最低可定价为多少元?
(1)这种水果批发商一共购买了多少千克?
(2)该批发商将货物运回邻市批发销售.已知在运输途中水果有15%的损耗,运费为820元,为使获得的利润不低于2200元,该批发商的批发价最低可定价为多少元?
考点:分式方程的应用,一元一次不等式的应用
专题:
分析:(1)设这种水果在甲果园定购了x千克,那么乙果园定购了
x千克,根据单价乙比在甲果园购买的要贵0.1元/千克,可列方程求解.
(2)设该批发商的批发价定价为y元,根据获得的利润不低于2200元,可列不等式求解.
| 1 |
| 2 |
(2)设该批发商的批发价定价为y元,根据获得的利润不低于2200元,可列不等式求解.
解答:解:(1)设这种水果在甲果园定购了x千克,那么乙果园定购了
x千克,依题意有
-
=0.1,
解得x=2000,
x=1000,
2000+1000=3000(千克).
答:这种水果批发商一共购买了3000千克.
(2)设该批发商的批发价定价为y元,依题意有
3000×(1-15%)y≥2000+1100+820+2200,
解得y≥2.4.
答:该批发商的批发价最低可定价为2.4元.
| 1 |
| 2 |
| 1100 | ||
|
| 2000 |
| x |
解得x=2000,
| 1 |
| 2 |
2000+1000=3000(千克).
答:这种水果批发商一共购买了3000千克.
(2)设该批发商的批发价定价为y元,依题意有
3000×(1-15%)y≥2000+1100+820+2200,
解得y≥2.4.
答:该批发商的批发价最低可定价为2.4元.
点评:本题考查分式方程的应用和一元一次不等式的应用,以及理解题意的能力,关键找到以钱数为等量关系和不等量关系,列方程和不等式求解.

练习册系列答案
相关题目
在平面直角坐标系中,下面的点在第四象限的是( )
| A、(1,3) |
| B、(0,-3) |
| C、(4,-1) |
| D、(-2,-3) |
 如图,在△ABC中,∠C=90°,D是AC边上一点,且AD=BD=5,tan∠CBD=
如图,在△ABC中,∠C=90°,D是AC边上一点,且AD=BD=5,tan∠CBD= 如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME. 如图,菱形ABCD中,点M为AD的中点,点N在AB上,DE⊥BC的延长线于点E,连接BM、DN、EN,∠AND=∠MBC.
如图,菱形ABCD中,点M为AD的中点,点N在AB上,DE⊥BC的延长线于点E,连接BM、DN、EN,∠AND=∠MBC.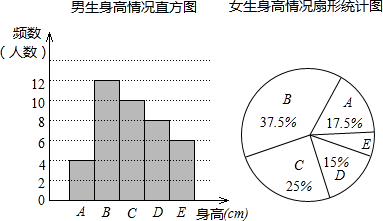 抽样检查,已知抽取的样本中,男生女生的人数相同,利用所得数据绘制如下统计图表:
抽样检查,已知抽取的样本中,男生女生的人数相同,利用所得数据绘制如下统计图表: