题目内容
二次函数y=ax2＋bx＋c(a≠0)的图象如图所示，根据图象解答下列问题．
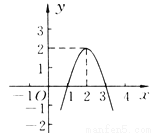
(1)写出方程ax2＋bx＋c＝0的两个根；
(2)写出不等式ax2＋bx＋c＞0的解集；
(3)写出y随x的增大而减小的自变量x的取值范围；
(4)若方程ax2＋bx＋c＝k有两个不相等的实数根，求k的取值范围．
（1）x＝1或x＝3是方程ax2＋bx＋c＝0的两个根；（2）l＜x＜3；（3）当x＞2时，y随x的增大而减小；（4）k＜2．
【解析】试题分析：（1）观察图形可以看出抛物线与x轴交于（1，0）和（3，0），即可解题
（2）根据抛物线y=ax2+bx+c，求得y＞0的x取值范围即可解题；
（3）图中可以看出抛物线对称轴，即可解题；
（3）易求得抛物线解析式，根据方程△＞0即...
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案△ABC中，AB=AC，∠A=36°，∠ABC和∠ACB的平分线BE、CD交于点F，则共有等腰三角形( ）
A. 7个 B. 8个 C. 9个 D. 10个
B
【解析】∵等腰三角形有两个角相等，
∴只要能判断出有两个角相等就行了，
将原图各角标上后显示如左下：
因此，所有三角形都是等腰三角形，
只要判断出有哪几个三角形就可以了.
如右上图，三角形有如下几个：
①，②，③；①+②，③+②，①+④，③+④；①+②+③+④；共计8个.
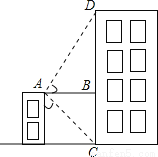
故选：B. 从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（ ）
A．（6+6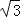
）米 B．（6+3
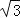）米 C．（6+2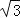）米 D．12米
A
【解析】
试题分析：在Rt△ACB中，∠CAB=45°，AB⊥DC，AB=6，
∴BC=AB=6，
在Rt△ABD中，∵tan∠BAD=，
∴BD=AB•tan∠BAD=6，
∴DC=CB+BD=6+6（m）．
故选A． 如图所示，桥拱是抛物线形，其函数的表达式为y= -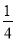
x2，当水位线在AB位置时，水面宽12m，这时水面离桥顶的高度为（ ）
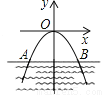
A. 3m B.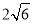 
m C.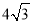 
m D. 9 m
D
【解析】试题解析：由已知知：
点的横坐标为.
把代入
得
即水面离桥顶的高度为
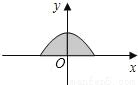
故选D. 如图所示是二次函数y=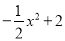
的图象在x轴上方的一部分，对于这段图象与x轴所围成的阴影部分的面积，你认为可能的值是（ ）
A. 4 B.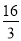 
C. 2π D. 8
B
【解析】函数与y轴交于（0，2）点，与x轴交于（-2，0）和（2，0）两点，则三点构成的三角形面积S1=4，则以半径为2的半圆的面积为S2=π××22=2π，则阴影部分的面积S有：4＜S＜2π．因为选项A、C、D均不在S取值范围内．故选 B 已知二次函数y=-x2+4x-3，其图象与y轴交于点B，与x轴交于A，C 两点.求△ABC的周长和面积.
C△ABC=，S△ABC=3.
【解析】试题分析：先分别求得二次函数的图象与坐标轴的交点坐标，再根据勾股定理求得△ABC的三边长，即可得到△ABC的周长，再根据三角形的面积公式即可求得结果.
令x=0,得y=-3,故B点坐标为(0,-3).
解方程-x2+4x-3=0,得x1=1,x2=3.
故A、C两点的坐标为(1,0),(3,0).
所以AC=3-1=2,AB=,... 函数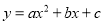
的图象如图所示，则下列结论错误的是（ ）
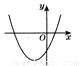
A. a＞0 B. b2－4ac＞0
C.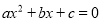 
的两根之和为负 D. 
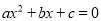的两根之积为正
D
【解析】【解析】
∵抛物线开口向上，∴a＞0，故A正确．
∵抛物线与x轴有两个交点，∴b2－4ac＞0，故B正确．
由图象可知， 一根为正，一根为负，且负根的绝对值大于正根的绝对值，∴两根之和为负，两根之积为负，故C正确，D错误．
故选D． 已知二次函数y＝－x2＋4，当－2≤x≤3时，函数的最小值是_____，最大值是____．
－5 4
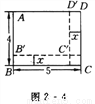
【解析】试题解析：抛物线y＝－x2＋4，开口向下，有最大值为4，当x=3时有最小值为-5. 如图2 - 4所示，长方形ABCD的长为5 cm，宽为4 cm，如果将它的长和宽都减去x(cm)，那么它剩下的小长方形AB′C′D′的面积为y(cm2)．
(1)写出y与x的函数关系式；
(2)上述函数是什么函数?
(3)自变量x的取值范围是什么?
(1) y＝x2－9x＋20；(2) 二次函数;(3) 0＜x＜4.
【解析】试题分析：（1）根据长方形的面积公式，根据图示求解即可得到函数关系式；
（2）通过二次函数的定义可判断；
（3）根据x取值不能大于原方程的长方形的宽进行分析.
试题解析：(1)根据长方形的面积公式，得y＝(5－x)·(4－x)＝x2－9x＋20，所以y与x的函数关系式为y＝x2－9x＋20．
...