题目内容
如下图，与①中的三角形相比，②中的三角形发生的变化是（ ）
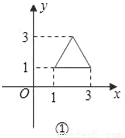
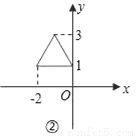
A. 向左平移3个单位 B. 向左平移2个单位
C. 向上平移3个单位 D. 向上平移1个单位
A
【解析】【解析】
由图①到图②，点（1，1）平移到点（﹣2，1），
点（3，1）平移到点（0，1），都是向左平移3个单位，
∴图形平移规律为：向左平移3个单位．
故选A．
鹰派教辅衔接教材河北教育出版社系列答案如图，△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线交AB于E，D为垂足，连接EC.
求∠ECD的度数；
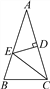
36°
【解析】试题分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AE=CE，然后根据等边对等角可得∠ECD=∠A；
试题解析：
∵ED垂直平分AC，
∴AE=CE，
∴∠ECD=∠A，
∵∠A=36°，
∴∠ECD=36°； 利用因式分解简便计算（要求写出完整计算过程）
(1) 
（2）
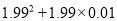
(1)800;(2)3.98.
【解析】试题分析：（1）利用平方差公式得到原式=（201+199）×（201-199），然后进行有理数运算；
（2）利用提公因式得到原式=1.99×（1.99+0.01），然后进行有理数运算．
试题解析：（1）原式=（201+199）×（201-199）
=400×2
=800；
（2）原式=1.99×（1.99+0.01）
... 不论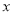
, 
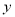为任何实数， 
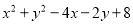的值总是（ ）
A. 正数 B. 负数 C. 非负数 D. 非正数
A
【解析】x²+y²－4x-2y+8=(x²－4x+4)+(y²-2y+1)+3=(x-2)2+(y-1)2+3≥3，
不论x,y为任何实数,x²+y²－4x-2y+8的值总是大于等于3，
故选A. 如图，A、B两点的坐标分别为(2,3)、(4,1)．
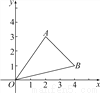
(1)求△ABO的面积；
(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′，求△O′A′B′的3个顶点的坐标．
（1）S△ABO＝5；（2）A′(2,0)，B′(4，－2)，O′(0，－3)．
【解析】试题分析:(1)利用面积的割补法求解,(2)根据点的平移规律,向下平移,横坐标不变,纵坐标减去平移得单位长度即可求解.
试题解析:(1)如图所示:S△ABO＝3×4－×3×2－×4×1－×2×2＝5,
(2)A′(2,0),B′(4,－2),O′(0,－3)． 如图，直线l1在平面直角坐标系中，直线l1与y轴交于点A，点B(－3,3)也在直线l1上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C恰好也在直线l1上．
(1)求点C的坐标和直线l1的解析式；
(2)若将点C先向左平移3个单位长度，再向上平移6个单位长度得到点D，请你判断点D是否在直线l1上；
(3)已知直线l2：y＝x＋b经过点B，与y轴交于点E，求△ABE的面积．
(1) C的坐标为(－2,1)，直线l1的解析式为y＝－2x－3；(2)点D在直线l1上；(3)△ABE的面积为13.5.
【解析】试题分析：（1）∵B（﹣3，3），将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，
∴﹣3+1=﹣2，3﹣2=1，∴C的坐标为（﹣2，1），设直线l1的解析式为y=kx+c，∵点B、C在直线l1上，∴代入得：，解得：k=﹣2，c=﹣3，∴直线... 在平面直角坐标中，△ABC的三个顶点的坐标分别是A(－2,3)，B(－4，－1)，C(2,0)，将△ABC沿x轴方向向左平移_______至△A1B1C1的位置，点A、B、C的对应点分别是A1、B1、C1，使点C1在原点处．
2个单位
【解析】因为C(2,0)沿x轴方向向左平移后对应对应点C1在原点处,即点C沿x轴方向向左平移2个单位,故答案为:2. 下列哪一个函数，其图象与x轴有两个交点（ ）
A. y=(x-23)2+155 B. y=(x+23)2+155
C. y= -(x-23)2-155 D. y= -(x+23)2+155
D
【解析】A、令y=0得，(x-23)2+155=0，移项得，(x-23)2= -155，方程无实根；
B、令y=0得，(x+23)2+155=0，移项得，(x+23)2= -155，方程无实根；
C、令y=0得，-(x-23)2-155=0，移项得，(x-23)2= -155，方程无实根；
D、令y=0得，-(x+23)2+155=0，移项得，(x+23)2=155，方... △ABC中，AB=AC，∠A=36°，∠ABC和∠ACB的平分线BE、CD交于点F，则共有等腰三角形( ）
A. 7个 B. 8个 C. 9个 D. 10个
B
【解析】∵等腰三角形有两个角相等，
∴只要能判断出有两个角相等就行了，
将原图各角标上后显示如左下：
因此，所有三角形都是等腰三角形，
只要判断出有哪几个三角形就可以了.
如右上图，三角形有如下几个：
①，②，③；①+②，③+②，①+④，③+④；①+②+③+④；共计8个.
故选：B.