题目内容
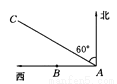
如图所示，某货船以20海里／时的速度将一批重要物资由A处运往正西方向的B处，经16小时到达，到达后立即卸货，此时接到气象部门通知，一台风中心正以40海里／时的速度由A处向北偏西60°的AC方向移动，距台风中心200海里的圆形区域(包括边界)均会受到影响：
(1)B处是否会受到台风的影响?清说明理由；
(2)为避免卸货过程受到台风影响，船上人员应在多少小时内卸完货物?(精确到0.1小时，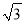 
≈1.732)
（1）B处会受到台风的影响（2）在3.9小时内卸完货才不会受台风影响
【解析】试题分析：(1)、过B作BD⊥AC于D，根据Rt△ABD的性质得出BD的长度，从而得出答案；(2)、以B为圆心，200海里为半径画圆交AC于E，F两点，连接BE，BF，根据垂径定理得出DE的长度，从而求出AE的长度，最后求出时间．
试题解析：(1)、如图所示，过B作BD⊥AC于D，在Rt△ABD中，
B...
天天向上一本好卷系列答案
小学生10分钟应用题系列答案下列哪一个函数，其图象与x轴有两个交点（ ）
A. y=(x-23)2+155 B. y=(x+23)2+155
C. y= -(x-23)2-155 D. y= -(x+23)2+155
D
【解析】A、令y=0得，(x-23)2+155=0，移项得，(x-23)2= -155，方程无实根；
B、令y=0得，(x+23)2+155=0，移项得，(x+23)2= -155，方程无实根；
C、令y=0得，-(x-23)2-155=0，移项得，(x-23)2= -155，方程无实根；
D、令y=0得，-(x+23)2+155=0，移项得，(x+23)2=155，方... △ABC中，AB=AC，∠A=36°，∠ABC和∠ACB的平分线BE、CD交于点F，则共有等腰三角形( ）
A. 7个 B. 8个 C. 9个 D. 10个
B
【解析】∵等腰三角形有两个角相等，
∴只要能判断出有两个角相等就行了，
将原图各角标上后显示如左下：
因此，所有三角形都是等腰三角形，
只要判断出有哪几个三角形就可以了.
如右上图，三角形有如下几个：
①，②，③；①+②，③+②，①+④，③+④；①+②+③+④；共计8个.
故选：B. 已知△ABC中，AB＝AC，求证∠B＜90°，下面写出了用反证法证明过程中的四个步骤：①所以∠B＋∠C＋∠A＞180°，这与三角形内角和定理相矛盾；②所以∠B＜90°；③假设∠B≥90°；④那么由AB＝AC，得∠B＝∠C≥90°，即∠B＋∠C≥180°.这四个步骤正确的顺序应是_________(填序号)．
③④①②
【解析】试题分析：利用反证法来进行证明时，首先假设结论不成立，然后根据已知条件得出与定理相矛盾，最后得出假设不成立，得出答案，故正确的序号是：③④①②． 如图所示，已知OC平分∠AOB，CD∥OB，若OD＝3cm，则CD等于( )
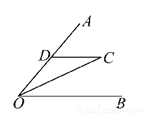
A. 3cm B. 4cm C. 1.5cm D. 2cm
A
【解析】试题分析：根据角平分线的性质可得：∠DOC=∠COB，根据平行线的性质可得：∠DCO=∠COB，则∠DOC=∠DCO，则CD=OD=3cm，故选A． 如图，小山顶上有一信号塔AB，山坡BC的倾角为30°，现为了测量塔高AB，测量人员选择山脚C处为一测量点，测得塔顶仰角为45°，然后顺山坡向上行走100米到达E处，再测得塔顶仰角为60°，求塔高AB.（结果保留整数
）
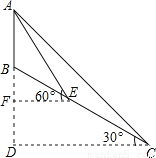
塔高AB大约为58米
【解析】【解析】
依题意可得：∠AEB=30°，∠ACE=15°，
又∵∠AEB=∠ACE+∠CAE，∴∠CAE=15°。
∴△ACE为等腰三角形。∴AE=CE=100米。
在Rt△AEF中，∠AEF=60°，∴EF=AEcos60°=50（米），AF=AEsin60°=50（米）。
在Rt△BEF中，∠BEF=30°，∴BF=EFtan30°... 从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（ ）
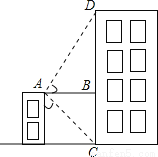
A．（6+6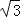
）米 B．（6+3
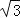）米 C．（6+2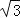）米 D．12米
A
【解析】
试题分析：在Rt△ACB中，∠CAB=45°，AB⊥DC，AB=6，
∴BC=AB=6，
在Rt△ABD中，∵tan∠BAD=，
∴BD=AB•tan∠BAD=6，
∴DC=CB+BD=6+6（m）．
故选A． 如图所示，桥拱是抛物线形，其函数的表达式为y= -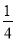
x2，当水位线在AB位置时，水面宽12m，这时水面离桥顶的高度为（ ）
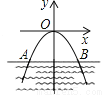
A. 3m B.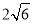 
m C.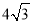 
m D. 9 m
D
【解析】试题解析：由已知知：
点的横坐标为.
把代入
得
即水面离桥顶的高度为
故选D. 已知二次函数y＝－x2＋4，当－2≤x≤3时，函数的最小值是_____，最大值是____．
－5 4
【解析】试题解析：抛物线y＝－x2＋4，开口向下，有最大值为4，当x=3时有最小值为-5.