题目内容
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,求x为何值时 y=1?
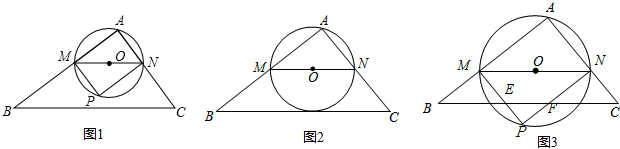
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,求x为何值时 y=1?

考点:圆的综合题
专题:
分析:(1)由于三角形PMN和AMN的面积相当,那么可通过求三角形AMN的面积来得出三角形PMN的面积,求三角形AMN的面积可根据三角形AMN和ABC相似,根据相似比的平方等于面积比来得出三角形AMN的面积;
(2)当圆O与BC相切时,O到BC的距离就是MN的一半,那么关键是求出MN的表达式,可根据三角形AMN和三角形ABC相似,得出MN的表达式,也就求出了O到BC的距离的表达式,如果过M作MQ⊥BC于Q,那么MQ就是O到BC的距离,然后在直角三角形BMQ中,用∠B的正弦函数以及BM的表达式表示出MQ,然后让这两表示MQ的含x的表达式相等,即可求出x的值;
(3)要求重合部分的面积首先看P点在三角形ABC内部还是外面,因此可先得出这两种情况的分界线即当P落到BC上时,x的取值,那么P落点BC上时,MN就是三角形ABC的中位线,此时AM=2,因此可分两种情况进行讨论:
①当0<x≤2时,此时重合部分的面积就是三角形PMN的面积,三角形PMN的面积(1)中已经求出,即可的x,y的函数关系式.②当2<x<4时,如果设PM,PN交BC于E,F,那么重合部分就是四边形MEFN,可通过三角形PMN的面积-三角形PEF的面积来求重合部分的面积.不难得出PN=AM=x,而四边形BMNF又是个平行四边形,可得出FN=BM,也就有了FN的表达式,就可以求出PF的表达式,然后参照(1)的方法可求出三角形PEF的面积,即可求出四边形MEFN的面积,也就得出了y,x的函数关系式,进而求出x的值.
(2)当圆O与BC相切时,O到BC的距离就是MN的一半,那么关键是求出MN的表达式,可根据三角形AMN和三角形ABC相似,得出MN的表达式,也就求出了O到BC的距离的表达式,如果过M作MQ⊥BC于Q,那么MQ就是O到BC的距离,然后在直角三角形BMQ中,用∠B的正弦函数以及BM的表达式表示出MQ,然后让这两表示MQ的含x的表达式相等,即可求出x的值;
(3)要求重合部分的面积首先看P点在三角形ABC内部还是外面,因此可先得出这两种情况的分界线即当P落到BC上时,x的取值,那么P落点BC上时,MN就是三角形ABC的中位线,此时AM=2,因此可分两种情况进行讨论:
①当0<x≤2时,此时重合部分的面积就是三角形PMN的面积,三角形PMN的面积(1)中已经求出,即可的x,y的函数关系式.②当2<x<4时,如果设PM,PN交BC于E,F,那么重合部分就是四边形MEFN,可通过三角形PMN的面积-三角形PEF的面积来求重合部分的面积.不难得出PN=AM=x,而四边形BMNF又是个平行四边形,可得出FN=BM,也就有了FN的表达式,就可以求出PF的表达式,然后参照(1)的方法可求出三角形PEF的面积,即可求出四边形MEFN的面积,也就得出了y,x的函数关系式,进而求出x的值.
解答:解:(1)∵MN∥BC,
∴∠AMN=∠B,∠ANM=∠C.
∴△AMN∽△ABC.
∴
=
,即
=
;
∴AN=
x;
∴S=S△MNP=S△AMN=
•
x•x=
x2.(0<x<4)
(2)如答题图1,
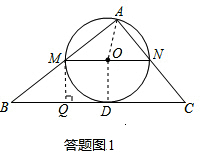
设直线BC与⊙O相切于点D,连接AO,OD,则AO=OD=
MN.
在Rt△ABC中,BC=
=5;
由(1)知△AMN∽△ABC,
∴
=
=
,即
=
,
∴MN=
x
∴OD=
x,
过M点作MQ⊥BC于Q,则MQ=OD=
x,
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA,
∴
=
,
∴BM=
=
x,AB=BM+MA=
x+x=4
∴x=
,
故当x=
时,⊙O与直线BC相切;,
(3)如答题图2,随点M的运动,当P点落在直线BC上时,连接AP,则O点为AP的中点.
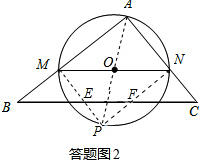
∵MN∥BC,
∴∠AMN=∠B,∠AOM=∠APB,
∴△AMO∽△ABP,
∴
=
=
,
∵AM=MB=2,
故以下分两种情况讨论:
①当0<x≤2时,y=S△PMN=
x2,
∴当y=1时,x=
或x=-
(不合题意舍去),
②当2<x<4时,设PM,PN分别交BC于E,F,
∵四边形AMPN是矩形,
∴PN∥AM,PN=AM=x,
又∵MN∥BC,
∴四边形MBFN是平行四边形;
∴FN=BM=4-x,
∴PF=x-(4-x)=2x-4,
又∵△PEF∽△ACB,
∴(
)2=
,
∴S△PEF=
(x-2)2;
y=S△MNP-S△PEF=
x2-
(x-2)2=-
x2+6x-6,
当2<x<4时,y=-
x2+6x-6,
∴当y=1时,x1=
,x2=
(不合题意舍去),
综上所述,当x的值是
或
时,y的值为1.
∴∠AMN=∠B,∠ANM=∠C.
∴△AMN∽△ABC.
∴
| AM |
| AB |
| AN |
| AC |
| x |
| 4 |
| AN |
| 3 |
∴AN=
| 3 |
| 4 |
∴S=S△MNP=S△AMN=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
(2)如答题图1,

设直线BC与⊙O相切于点D,连接AO,OD,则AO=OD=
| 1 |
| 2 |
在Rt△ABC中,BC=
| AB2+AC2 |
由(1)知△AMN∽△ABC,
∴
| AM |
| AB |
| AO |
| AP |
| 1 |
| 2 |
| x |
| 4 |
| MN |
| 5 |
∴MN=
| 5 |
| 4 |
∴OD=
| 5 |
| 8 |
过M点作MQ⊥BC于Q,则MQ=OD=
| 5 |
| 8 |
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA,
∴
| BM |
| BC |
| QM |
| AC |
∴BM=
5×
| ||
| 3 |
| 25 |
| 24 |
| 25 |
| 24 |
∴x=
| 96 |
| 49 |
故当x=
| 96 |
| 49 |
(3)如答题图2,随点M的运动,当P点落在直线BC上时,连接AP,则O点为AP的中点.

∵MN∥BC,
∴∠AMN=∠B,∠AOM=∠APB,
∴△AMO∽△ABP,
∴
| AM |
| AB |
| AO |
| AP |
| 1 |
| 2 |
∵AM=MB=2,
故以下分两种情况讨论:
①当0<x≤2时,y=S△PMN=
| 3 |
| 8 |
∴当y=1时,x=
2
| ||
| 3 |
2
| ||
| 3 |
②当2<x<4时,设PM,PN分别交BC于E,F,
∵四边形AMPN是矩形,
∴PN∥AM,PN=AM=x,
又∵MN∥BC,
∴四边形MBFN是平行四边形;
∴FN=BM=4-x,
∴PF=x-(4-x)=2x-4,
又∵△PEF∽△ACB,
∴(
| PF |
| AB |
| S△PEF |
| S△ABC |
∴S△PEF=
| 3 |
| 2 |
y=S△MNP-S△PEF=
| 3 |
| 8 |
| 3 |
| 2 |
| 9 |
| 8 |
当2<x<4时,y=-
| 9 |
| 8 |
∴当y=1时,x1=
8+2
| ||
| 3 |
8-2
| ||
| 3 |
综上所述,当x的值是
2
| ||
| 3 |
8+2
| ||
| 3 |
点评:本题主要考查了相似三角形的性质以及二次函数的综合应用,要注意(3)中要根据P点的位置的不同分情况进行讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方形ABCD的边长是8cm,以正方形的中心O为圆心,EF为直径的半圆切AB于M、切BC于N,已知C为BG的中点,AG交CD于H.P,Q同时从A出发,P以1cm/s的速度沿折线ADCG运动,Q以
如图,正方形ABCD的边长是8cm,以正方形的中心O为圆心,EF为直径的半圆切AB于M、切BC于N,已知C为BG的中点,AG交CD于H.P,Q同时从A出发,P以1cm/s的速度沿折线ADCG运动,Q以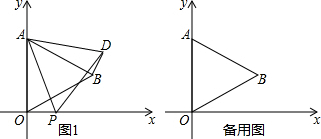
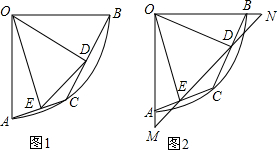 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.