题目内容
7.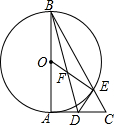 如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F
如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F(1)求证:DE所在的直线为⊙O的切线.
(2)若AB=10,BE=5$\sqrt{3}$,求OF的长.
分析 (1)连接OD,证AD=DE,证△OAD≌△OED,∠OED=∠OAD=90°即可.
(2)连接AE,根据勾股定理得到AE=5,得到AE=$\frac{1}{2}$AB,由AB是⊙O的直径,得到∠AEB=90°,求得∠ABC=30°,得到BC=$\frac{20\sqrt{3}}{3}$,根据三角形中位线的想知道的OD∥BC,OD=$\frac{1}{2}$BC=$\frac{10\sqrt{3}}{3}$,于是得到OD:BE=OF:EF=2:3;即可得到结论.
解答 (1)证明:连接OD;如图1所示: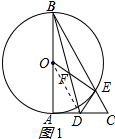
∵O、D分别是AB、AC的中点,
∴OD∥BC,
∴∠AOD=∠ABC,∠DOE=∠BEO;
∵OB=OE,
∴∠AOD=∠DOE,
在△OAD和△OED中,$\left\{\begin{array}{l}{OA=OE}\\{∠AOD=∠DOE}\\{OD=OD}\end{array}\right.$,
∴△OAD≌△OED(SAS),
∴∠OED=∠OAD=90°,DE=AD,
∴DE为⊙O的切线.
(2)解:连接AE,如图2所示: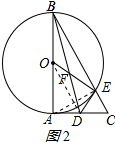
∵AB=10,BE=5$\sqrt{3}$,
∴AE=5,
∴AE=$\frac{1}{2}$AB,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠ABC=30°,
∴BC=$\frac{20\sqrt{3}}{3}$,
∵OD∥BC,OD=$\frac{1}{2}$BC=$\frac{10\sqrt{3}}{3}$,
∴OD:BE=OF:EF=2:3;
∵OE=$\frac{1}{2}$AB=5,
∴OF=2.
点评 本题考查了切线的判定,勾股定理和三角形全等的判定,三角函数,相似三角形的判定与性质等知识点.熟练掌握切线的判定,由勾股定理求出AD是解决问题(2)的关键.

| A. | (-$\frac{1}{2}$,1) | B. | (2,-1) | C. | (-1,2) | D. | (1,$\frac{1}{2}$) |
| A. | a>-$\frac{1}{5}$ | B. | -$\frac{1}{5}$<a<0 | C. | a<$\frac{1}{5}$ | D. | 0<a<$\frac{1}{5}$ |
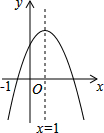 已知二次函数的图象如图,则下列结论中正确的有( )
已知二次函数的图象如图,则下列结论中正确的有( )①a+b+c>0;②a-b+c<0;③b>0;④b=2a;⑤abc<0.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
| A. | a=5,b=1 | B. | a=-5,b=1 | C. | a=5,b=-1 | D. | a=-5,b=-1 |
| A. | k<1 | B. | k>1 | C. | k<-1 | D. | k>-1 |
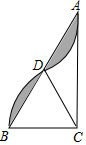 如图,在Rt△ABC中,∠ACB=90°,AC=4$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为$\frac{16}{3}$π-8$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,AC=4$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为$\frac{16}{3}$π-8$\sqrt{3}$. 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P90的坐标是(30,0).
如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P90的坐标是(30,0).