题目内容
17.已知关于x的方程x2+2x+k=0没有实数根,则k的取值范围是( )| A. | k<1 | B. | k>1 | C. | k<-1 | D. | k>-1 |
分析 根据方程的系数结合根的判别式,即可得出△=4-4k<0,解之即可得出结论.
解答 解:∵关于x的方程x2+2x+k=0没有实数根,
∴△=22-4k=4-4k<0,
解得:k>1.
故选B.
点评 本题考查了根的判别式以及解一元一次不等式,牢记“当△<0时,方程无实数根”是解题的关键.

练习册系列答案
相关题目
8.下列各数中,最小的数是( )
| A. | -$\frac{2}{3}$ | B. | -1 | C. | -|-$\sqrt{3}$| | D. | 3-2 |
5.若a<$\sqrt{10}$-1<b,且a,b是两个连续的整数,则a-b的值是( )
| A. | 9 | B. | 8 | C. | $\frac{1}{9}$ | D. | $\frac{1}{8}$ |
12.下列关于一次函数y=-2x+1的说法,其中正确的是( )
| A. | 图象经过第一、二、三象限 | B. | 图象经过点(-2,1) | ||
| C. | 当x>1时,y<0 | D. | y随x的增大而增大 |
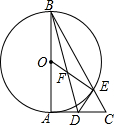 如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F
如图,在Rt△ABC中,∠BAC=90°.以AB为直径的⊙O交BC于点E,D为AC的中点.连接DE,BD与OE相交于点F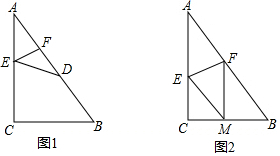
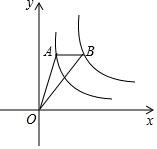 如图,点A是反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2-k1的值为( )
如图,点A是反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2-k1的值为( )