题目内容
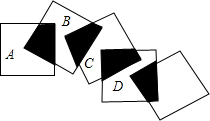 如图,将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,则图中四块阴影面积的总和是( )
如图,将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,则图中四块阴影面积的总和是( )| A、1 | B、2 | C、3 | D、4 |
考点:正方形的性质,全等三角形的判定与性质,中心对称
专题:
分析:根据正方形的中心对称性,每一个阴影部分的面积等于正方形面积的
,四块阴影面积的总和正好等于一个正方形的面积,然后列式计算即可得解.
| 1 |
| 4 |
解答:解:由正方形的性质得,一个阴影部分的面积等于正方形的面积的
,
所以,四块阴影面积的总和正好等于一个正方形的面积,
∵五个正方形的边长都为2cm,
∴四块阴影面积的总和=22=4cm2.
故选:D.
| 1 |
| 4 |
所以,四块阴影面积的总和正好等于一个正方形的面积,
∵五个正方形的边长都为2cm,
∴四块阴影面积的总和=22=4cm2.
故选:D.
点评:本题考查了正方形的性质,熟记中心对称性判断出每一个阴影部分的面积等于正方形的面积的
是解题的关键.
| 1 |
| 4 |

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
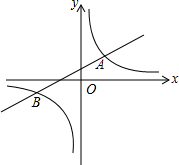 如图,一次函数y1=k1+2与反比例函数y2=
如图,一次函数y1=k1+2与反比例函数y2=| k2 |
| x |
| A、x<-8或0<x<4 |
| B、x>4或-8<x<0 |
| C、-8<x<4 |
| D、x<-8或x>4 |
三角形的周长为56cm,则它的三条中位线组成的三角形的周长是( )
| A、18cm | B、28cm |
| C、24cm | D、36cm |
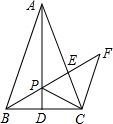 如图,在△ABC中,AB=AC,D是BC中点.CF∥AB,BF分别交AD、AC于点P、E.求证:BP是PE、PF的比例中项.
如图,在△ABC中,AB=AC,D是BC中点.CF∥AB,BF分别交AD、AC于点P、E.求证:BP是PE、PF的比例中项. 如图∠1=∠2,AB=10cm,AD:DB=2:3,那么AC=
如图∠1=∠2,AB=10cm,AD:DB=2:3,那么AC=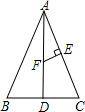 如图,△ABC中,AB=AC=10,BC=8,AD⊥BC于D,E为AC的中点,EF⊥AC于E,交AD于F,求EF的长度.
如图,△ABC中,AB=AC=10,BC=8,AD⊥BC于D,E为AC的中点,EF⊥AC于E,交AD于F,求EF的长度.