题目内容
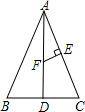 如图,△ABC中,AB=AC=10,BC=8,AD⊥BC于D,E为AC的中点,EF⊥AC于E,交AD于F,求EF的长度.
如图,△ABC中,AB=AC=10,BC=8,AD⊥BC于D,E为AC的中点,EF⊥AC于E,交AD于F,求EF的长度.考点:相似三角形的判定与性质,等腰三角形的性质
专题:
分析:由条件可得出Rt△ACD∽Rt△AEF,再利用线段比可求得EF的长.
解答:解:∵AB=AC=10,BC=8,AD⊥BC
∴DC=
BC=4,
在Rt△ADC中,由勾股定理可得AD=
=
=2
∵EF⊥AC,
∴∠ADC=∠AEF=90°,
且∠DAC=∠EAF,
∴Rt△ACD∽Rt△AEF,
∴
=
,
∵E为AC的中点,
∴AE=5,
∴
=
,
∴EF=
.
∴DC=
| 1 |
| 2 |
在Rt△ADC中,由勾股定理可得AD=
| AC2-DC2 |
| 102-42 |
| 21 |
∵EF⊥AC,
∴∠ADC=∠AEF=90°,
且∠DAC=∠EAF,
∴Rt△ACD∽Rt△AEF,
∴
| EF |
| CD |
| AE |
| AD |
∵E为AC的中点,
∴AE=5,
∴
| EF |
| 4 |
| 5 | ||
2
|
∴EF=
10
| ||
| 21 |
点评:本题主要考查相似三角形的判定和性质及等腰三角形的性质,由条件证得Rt△ACD∽Rt△AEF是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
(1)有理数中有最大的数;(2)有理数中没有最大的负整数;(3)只有负数的绝对值才是它的相反数;(4)最大的三位数与最小的三位数的和是1099;(5)小学时我们学的数都是正数.
在以上说法中正确的个数是( )
在以上说法中正确的个数是( )
| A、3个 | B、2个 | C、1个 | D、0个 |
在式子3>0,
a,3x=4,a-3b,4(x+y)中代数式的个数有( )
| 1 |
| 2 |
| A、5个 | B、4个 | C、3个 | D、2个 |
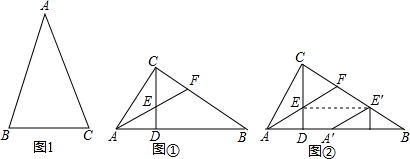
 如图,∠AOB=120°,AD⊥BD,CB⊥AC,AB=4,则DC=
如图,∠AOB=120°,AD⊥BD,CB⊥AC,AB=4,则DC=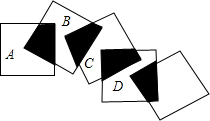 如图,将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,则图中四块阴影面积的总和是( )
如图,将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是这四个正方形的对角线的交点,则图中四块阴影面积的总和是( )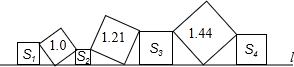 如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+2S2+2S3+S4=
如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+2S2+2S3+S4=