题目内容
11.将抛物线y=3x2通过平移得到抛物线y=3(x-1)2-2,下列平移方法正确的是( )| A. | 先向上平移2个单位长度,再向右平移1个单位长度 | |
| B. | 先向下平移2个单位长度,再向右平移1个单位长度 | |
| C. | 先向上平移2个单位长度,再向左平移1个单位长度 | |
| D. | 先向下平移2个单位长度,再向左平移1个单位长度 |
分析 原抛物线顶点坐标为(0,0),平移后抛物线顶点坐标为(1,-2),由此确定平移规律.
解答 解:y=3(x-1)2-2,该抛物线的顶点坐标是(1,-2),抛物线y=x2的顶点坐标是(0,0),
则平移的方法可以是:将抛物线y=3x2向下移2个单位,再向右平移1个单位.
故选:B.
点评 本题考查了二次函数图象与几何变换.关键是将抛物线的平移问题转化为顶点的平移,寻找平移方法.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
6. 如图,为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为α,那么楼房BC的高为( )米.
如图,为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为α,那么楼房BC的高为( )米.
 如图,为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为α,那么楼房BC的高为( )米.
如图,为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为α,那么楼房BC的高为( )米.| A. | $\frac{10}{sinα}$ | B. | $\frac{10}{tanα}$ | C. | 10sinα | D. | 10tanα |
20.△ABC的三边满足AC2-BC2=AB2,那么这个三角形的三个内角中( )
| A. | ∠A=90° | B. | ∠B=90° | C. | ∠C=90° | D. | 没有直角 |
1.读取表格中的信息,解决问题:
(1)计算:a1+b1+c1=3$\sqrt{2}$+3$\sqrt{3}$+3;
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
| n=1 | a1=$\sqrt{2}$+2$\sqrt{3}$ | b1=$\sqrt{3}$+2 | c1=1+2$\sqrt{2}$ |
| n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
| n=3 | a3=b2+2c2 | b3=c2+2a2 | c3=a2+2b2 |
| … | … | … | … |
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
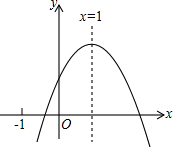 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有下列结论: 如图,二次函数y=-x2-2x的图象与x轴交于点A,O,在抛物线上有一点P,满足S△AOP=3,则点P的坐标是(1,-3)或(-3,-3).
如图,二次函数y=-x2-2x的图象与x轴交于点A,O,在抛物线上有一点P,满足S△AOP=3,则点P的坐标是(1,-3)或(-3,-3).