题目内容
13. 如图,在矩形ABCD中,E、F为边CD上的两点,且DE=EF=FC,连结AE、BF,并延长AE,BF相交于G
如图,在矩形ABCD中,E、F为边CD上的两点,且DE=EF=FC,连结AE、BF,并延长AE,BF相交于G(1)求证:AE=BF;
(2)若EG=3,求线段AE的长.
分析 (1)根据矩形的性质求出∠D=∠C=90°,AD=BC,根据全等三角形的判定推出△ADE≌△BCF即可;
(2)根据矩形的性质得出AB∥CD,AB=CD,求出$\frac{EF}{AB}$=$\frac{1}{3}$,证△GEF∽△GAB,根据相似三角形的性质得出比例式,求出AG,即可得出答案.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠D=∠C=90°,AD=BC,
在△ADE和△BCF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠D=∠C}\\{DE=FC}\end{array}\right.$,
∴△ADE≌△BCF(SAS),
∴AE=BF;
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∵DE=EF=FC,
∴$\frac{EF}{AB}$=$\frac{1}{3}$,
∵AB∥CD,
∴△GEF∽△GAB,
∴$\frac{EG}{AG}$=$\frac{EF}{AB}$=$\frac{1}{3}$,
∵EG=3,
∴AG=9,
∴AE=9-3=6.
点评 本题考查了矩形的性质,全等三角形的性质和判定,相似三角形的性质和判定的应用,能推出△ADE≌△BCF和△GEF∽△GAB是解此题的关键,题目综合性比较强,难度适中.

练习册系列答案
相关题目
3.等腰三角形三边的长为2、2、b,若关于x的方程${x^2}-\sqrt{2}bx+1=0$的两根之差的绝对值为$2\sqrt{5}$,则等腰三角形的底角的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
8.若买2支圆珠笔、1本笔记本需14元;买1支圆珠笔,2本笔记本需16元,则买4支圆珠笔、4本笔记本需( )元.
| A. | 30 | B. | 32 | C. | 40 | D. | 42 |
2.当x=1时,代数式ax3-3ax+4的值是7,则当x=-1时,这个代数式的值是( )
| A. | 7 | B. | 3 | C. | 1 | D. | -7 |
3.不等式组$\left\{\begin{array}{l}{x+\frac{x+1}{2}>\frac{2x-9}{3}-\frac{x-3}{6}}\\{-\frac{1}{2}(1-2x)>1}\end{array}\right.$的解集是( )
| A. | x<-3 | B. | x>$\frac{3}{2}$ | C. | -3<x<$\frac{3}{2}$ | D. | 无解 |
 某服装网店李经理用11000元购进了甲、乙两种款式的童装共150件,两种童装的价格如右图所示,请你求出李经理购买甲乙两种款式的童装各多少件?
某服装网店李经理用11000元购进了甲、乙两种款式的童装共150件,两种童装的价格如右图所示,请你求出李经理购买甲乙两种款式的童装各多少件?
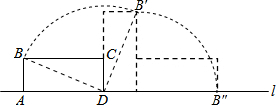 如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线上进行两次旋转,则点B在两次旋转过程中经过的路径的长是$\frac{25}{2}π$.
如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线上进行两次旋转,则点B在两次旋转过程中经过的路径的长是$\frac{25}{2}π$.