题目内容
11．
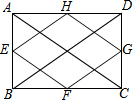如图，已知矩形ABCD的对角线AC，BD的长是6cm，E，F，G，H分别是AB，BC，CD，DA的中点，则四边形EFGH的周长是（ ）| A． | 18cm | B． | 16cm | C． | 15cm | D． | 12cm |
分析 根据三角形的中位线求出HG、GF、EF、EH的长，再求出四边形EFGH的周长即可．
解答 解：如图，∵四边形ABCD是矩形，
∴AC=BD=6cm，
∵E、F、G、H分别是AB、BC、CD、DA的中点，
∴HG=EF=$\frac{1}{2}$AC=3cm，EH=FG=$\frac{1}{2}$BD=3cm，
∴四边形EFGH的周长等于3cm+3cm+3cm+3cm=12cm，
故选：D．
点评 本题考查了矩形的性质，三角形的中位线的应用，能求出四边形的各个边的长是解此题的关键，注意：矩形的对角线相等，三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
阅读快车系列答案
相关题目
1．下列根式中属最简二次根式的是（ ）
| A． | $\sqrt{{a}^{2}+1}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{8}$ | D． | $\sqrt{4a+4}$ |
如图，在Rt△ABC中，∠C=90°．以点A为圆心、AC长为半径作圆弧，交边AB于点D．若∠B=65°，AC=6，则$\widehat{CD}$的长为$\frac{5}{6}$π．
如图，在?ABCD中，E、F分别为边AB、CD的中点，过A点作AG∥DB，交CB的延长线于点G．
6．
为了落实精准扶贫工作，省扶贫部门向了解某革命老区5000户居民的家庭经济状况，从中随机调查了40户家庭的月收入情况（收入区整数，单位：元），并绘制了如下的频数分布表和频数分布直方图（不完整）．
根据以上提供的信息，解答下列问题：
（1）表格中a=18，b=3，m=0.075；补全频数分布直方图；
（2）这40户家庭月收入的中位数落在哪一个小组？
（3）根据扶贫政策，要对月收入低于1000元的家庭进行精准扶贫，请你估计该革命老区符合政策的户数．
为了落实精准扶贫工作，省扶贫部门向了解某革命老区5000户居民的家庭经济状况，从中随机调查了40户家庭的月收入情况（收入区整数，单位：元），并绘制了如下的频数分布表和频数分布直方图（不完整）．根据以上提供的信息，解答下列问题：
| 组号 | 分组 | 频数 | 频率 |
| 1 | 600～799 | 2 | 0.050 |
| 2 | 800～999 | 6 | 0.150 |
| 3 | 1000～1999 | a | 0.450 |
| 4 | 1200～1399 | 9 | 0.225 |
| 5 | 1400～1599 | b | m |
| 6 | 1600～1799 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
（2）这40户家庭月收入的中位数落在哪一个小组？
（3）根据扶贫政策，要对月收入低于1000元的家庭进行精准扶贫，请你估计该革命老区符合政策的户数．
如图所示，OA⊥OC于点O，∠1=∠2，则∠BOD的度数是90°．