题目内容

9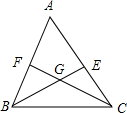．如图，已知△ABC的∠ABC和∠ACB的平分线BE，CF交于点G，若∠BGC=115°，则∠A=50°．

分析 根据三角形内角和定理求出∠GBC+∠GCB，根据角平分线的定义求出∠ABC+∠ACB，根据三角形内角和定理计算即可．

解答 解：∵∠BGC=115°，
∴∠GBC+∠GCB=180°-115°=65°，
∵BE，CF是△ABC的∠ABC和∠ACB的平分线，
∴∠GBC=$\frac{1}{2}∠$ABC，∠GCB=$\frac{1}{2}∠$ACB，
∴∠ABC+∠ACB=130°，
∴∠A=180°-130°=50°，
故答案为：50°．

点评 本题考查的是三角形内角和定理和角平分线的定义，掌握三角形内角和是180°是解题的关键．

练习册系列答案
相关题目
19．（1）计算：${（{-\frac{1}{3}}）^{-1}}-{（{2-\sqrt{3}}）^0}-4sin30°+\sqrt{12}$．
（2）化简（a+b）2-（a+2b）（a-2b）-2a（a-3b）．
20．某种铂金饰品在甲、乙两个商店销售．甲店标价：每克477元，按标价出售，不优惠；乙店标价：每克530元，但如果购买的铂金饰品质量超过3克，则超出的部分可打八折出售．设购买铂金饰品的质量为x克（x＞3），在甲店购买铂金饰品的费用为y甲元，在乙店购买铂金饰品的费用为y乙元．
（1）请分别求出y甲、y乙与x之间的函数关系式；
（2）当购买铂金饰品的质量是多少克时，甲乙两店的费用相等？
（3）当购买铂金饰品的质量是多少克时，在甲店购买比较合算？
（4）当购买铂金饰品的质量是多少克时，在乙店购买比较合算？
17．如右图，若AB∥CD，∠1=50°，则∠2的度数是（　　）
A．50°B．130°C．40°D．145°
4．如图，已知抛物线y=ax2+bx+c经过A（-2，-2），B（3，3），C（0，6）．
（1）求该抛物线的解析式．
（2）抛物线对称轴上是否存在点P，使△APC与△ABC的面积相等？若存在，求出点P的坐标；若不存在，说明理由．
（3）抛物线对称轴上是否存在点Q，使∠AQC=90°？若存在，求出Q点坐标；若不存在，说明理由．
14．如图，一组抛物线的顶点A1（x1，y1），A2（x2，y2），…An（xn，yn）（n为正整数）依次是反比例函数y=$\frac{9}{x}$图象上的点，第一条抛物线以A1（x1，y1）为顶点且过点O（0，0），B1（2，0），等腰△A1OB1为第一个三角形；第二条抛物线以A2（x2，y2）为顶点且经过点B1（2，0），B2（4，0），等腰△A2B1B2为第二个三角形；第三条抛物线以A3（x3，y3）为顶点且过点B2（4，0），B3（6，0），等腰△A3B2B3为第三个三角形；按此规律依此类推，…；第n条抛物线以An（xn，yn）为顶点且经过点Bn-1，Bn，等腰△AnBn-1Bn为第n个三角形．
（1）求出A1的坐标；
（2）求出第一条抛物线的解析式；
（3）请直接写出An的坐标（2n-1，$\frac{9}{2n-1}$）．
1．勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现；当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：

将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2
证明：连接DB，过点D作BC边上的高DF，
则DF=EC=b-a．
∵S四边形ADCB=S△ACD+S△ABC=$\frac{1}{2}$b2+$\frac{1}{2}$ab．
又∵S四边形ADCB=S△ADB+S△DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴a2+b2=c2
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．
求证：a2+b2=c2．
证明：连结BD，过点B作DE边上的高BF
∵S多边形ACBED=S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab
又∵S多边形ACBED=S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴a2+b2=c2．
18．4的算术平方根是2；9的平方根是±3；64的立方根是4．
19．解不等式组：$\left\{\begin{array}{l}{x-2＜1}\\{x+5≤2x+7}\end{array}\right.$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网