题目内容

10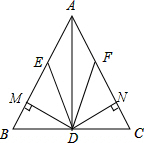．已知，如图，DE∥AC，DF∥AB，AE=AF，DM⊥AB于点M，DN⊥AC于N，求证：DM=DN．

分析 欲证明DM=DN，因为DM⊥AB于点M，DN⊥AC于N，所以只要证明∠BAC=∠CAD，可以通过证明四边形AEDF是菱形来实现．

解答 证明：∵DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形，
∵AE=AF，
∴四边形AEDF是菱形，
∴∠BAD=∠CAD，
∵DM⊥AB于点M，DN⊥AC于N，
∴DM=DN．

点评 本题考查菱形的判定和性质、角平分线的性质等知识，利用菱形的对角线平分一组对角这个性质证明角相等是解决这个问题的关键，属于中考常考题型．

练习册系列答案
相关题目
20．某种铂金饰品在甲、乙两个商店销售．甲店标价：每克477元，按标价出售，不优惠；乙店标价：每克530元，但如果购买的铂金饰品质量超过3克，则超出的部分可打八折出售．设购买铂金饰品的质量为x克（x＞3），在甲店购买铂金饰品的费用为y甲元，在乙店购买铂金饰品的费用为y乙元．
（1）请分别求出y甲、y乙与x之间的函数关系式；
（2）当购买铂金饰品的质量是多少克时，甲乙两店的费用相等？
（3）当购买铂金饰品的质量是多少克时，在甲店购买比较合算？
（4）当购买铂金饰品的质量是多少克时，在乙店购买比较合算？
1．勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现；当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：

将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2
证明：连接DB，过点D作BC边上的高DF，
则DF=EC=b-a．
∵S四边形ADCB=S△ACD+S△ABC=$\frac{1}{2}$b2+$\frac{1}{2}$ab．
又∵S四边形ADCB=S△ADB+S△DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴a2+b2=c2
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．
求证：a2+b2=c2．
证明：连结BD，过点B作DE边上的高BF
∵S多边形ACBED=S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab
又∵S多边形ACBED=S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴a2+b2=c2．
18．4的算术平方根是2；9的平方根是±3；64的立方根是4．
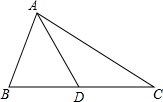5．已知如图，△ABC中，AB＜AC，D是BC中点，求证：∠CAD＜∠BAD．
15．若点Q（m，1-2m）的横坐标与纵坐标互为相反数，则点P一定在第四象限．
2．在-13，π，0，$\sqrt{3}$，2，-22，2.121121112…（两个2之间依次多一个1），0.3中．
（1）是有理数的有-13，0，2，-22，0.3；
（2）是无理数的有π，$\sqrt{3}$，2.121121112…（两个2之间依次多一个1）；
（3）是整数的有13，0，2，-22；
（4）是分数的有0.3．
19．解不等式组：$\left\{\begin{array}{l}{x-2＜1}\\{x+5≤2x+7}\end{array}\right.$．
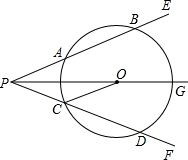20．如图所示，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF两边相交于A、B和C、D，连结OA，此时有OC∥PE
（1）求证：PC=OC；
（2）若弦CD=12，求tan∠OPD的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网