题目内容

6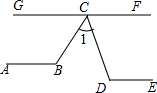．如图，AB∥DE∥GF，∠1：∠D：∠B=2：3：4，求∠1的度数？

分析 首先设∠1=2x°，∠D=3x°，∠B=4x°，根据两直线平行，同旁内角互补即可表示出∠GCB、∠FCD的度数，再根据∠GCB、∠1、∠FCD的为180°即可求得x的值，进而可得∠1的度数．

解答 解：∵∠1：∠D：∠B=2：3：4，
∴设∠1=2x°，∠D=3x°，∠B=4x°，
∵AB∥DE，
∴∠GCB=（180-4x）°，
∵DE∥GF，
∴∠FCD=（180-3x）°，
∵∠1+∠GCB+∠FCD=180°，
∴180-4x+2x+180-3x=180，
解得x=36，
∴∠1=72°．

点评 此题主要考查了平行线的性质，关键是掌握两直线平行，同旁内角互补．

练习册系列答案
相关题目
16．阅读下列材料：
我们定义：若一个四边形的一条对角线把四边形分成两个等腰三角形，则称这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如正方形，菱形都是和谐四边形．
结合阅读材料，完成下列问题：
如图，等腰Rt△ABD中，∠BAD=90°．若点C为平面上一点，AC为凸四边形ABCD的和谐线，且AB=BC，请画出图形并求出∠ABC的度数．
17．如右图，若AB∥CD，∠1=50°，则∠2的度数是（　　）
A．50°B．130°C．40°D．145°
14．如图，一组抛物线的顶点A1（x1，y1），A2（x2，y2），…An（xn，yn）（n为正整数）依次是反比例函数y=$\frac{9}{x}$图象上的点，第一条抛物线以A1（x1，y1）为顶点且过点O（0，0），B1（2，0），等腰△A1OB1为第一个三角形；第二条抛物线以A2（x2，y2）为顶点且经过点B1（2，0），B2（4，0），等腰△A2B1B2为第二个三角形；第三条抛物线以A3（x3，y3）为顶点且过点B2（4，0），B3（6，0），等腰△A3B2B3为第三个三角形；按此规律依此类推，…；第n条抛物线以An（xn，yn）为顶点且经过点Bn-1，Bn，等腰△AnBn-1Bn为第n个三角形．
（1）求出A1的坐标；
（2）求出第一条抛物线的解析式；
（3）请直接写出An的坐标（2n-1，$\frac{9}{2n-1}$）．
1．勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现；当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：

将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2
证明：连接DB，过点D作BC边上的高DF，
则DF=EC=b-a．
∵S四边形ADCB=S△ACD+S△ABC=$\frac{1}{2}$b2+$\frac{1}{2}$ab．
又∵S四边形ADCB=S△ADB+S△DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴a2+b2=c2
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．
求证：a2+b2=c2．
证明：连结BD，过点B作DE边上的高BF
∵S多边形ACBED=S△ACB+S△ABE+S△ADE=$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab
又∵S多边形ACBED=S△ACB+S△ABD+S△BDE=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴$\frac{1}{2}$ab+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a（b-a）
∴a2+b2=c2．
11．已知，AB∥CD，点P为AB、CD之间一点，连接AC．

（1）如图1，若AP平分∠BAC，CP平分∠ACD，求证：AP⊥CP；
（2）如图2，若∠PCD=2∠BAP，∠APC=90°，∠ACP=5∠PAC，延长AP交CD于点E，试探究∠PAC与∠AEC之间的数量关系，并说明理由．
（注意：本题不允许使用三角形内角和为180°）
18．4的算术平方根是2；9的平方根是±3；64的立方根是4．
15．若点Q（m，1-2m）的横坐标与纵坐标互为相反数，则点P一定在第四象限．
16．如图所示，与∠B构成同位角的共有（　　）
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网