题目内容
14.如图1,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将射线AC绕着点A顺时针旋转α(0°<α≤180°)得到射线AE,点M与点D关于直线AE对称.若$x=\frac{α}{15°}$,图中某点到点M的距离为y,表示y与x的函数关系的图象如图2所示,则这个点为图1中的( )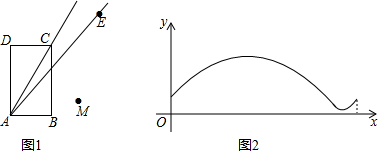
| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
分析 利用轴对称的性质进行分析图中A、B、C、D到点M的函数图象与图2中图象对比,即可得到答案.
解答 解:AM=$\sqrt{3}$,A不被选择.
当α=0°和α=30°时,BM值相等,不符合图2,B不被选择.
DM=2FM,y轴的刻度翻倍.波形的形状与图二相似,但y的最小值是0,故D不选择.
CM,见波形图.波形的形状与图二相似,y的最小值>0.比较之下,CM的波形接近图二.该点是C点.
故选:C.
点评 本题考查了轴对称的性质,函数的图象,数形结合.能利用数形结合综合分析是解决问题的关键.

练习册系列答案
相关题目
6. 如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )
如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )
 如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )
如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
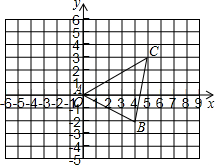 如图A、B、C是△ABC三个顶点
如图A、B、C是△ABC三个顶点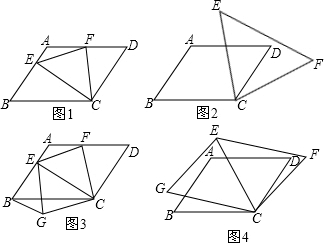
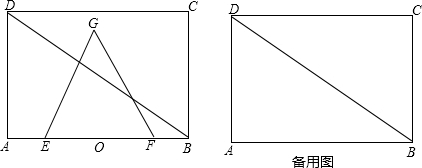
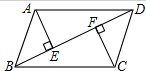 如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.
如图所示,?ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:AE=CF.