题目内容
2.点(-2,1)在反比例函数y=$\frac{k}{x}$的图象上,则k=-2;在图象的每一个分支上,y随x的增大而增大.分析 首先用待定系数法确定反比例函数的解析式,然后根据其性质确定其增减性即可.
解答 解:∵点(-2,1)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=-2×1=-2,
∵k<0,
∴在图象的每一个分支上,y随x的增大而增大,
故答案为:-2,增大.
点评 本题考查了反比例函数的性质,解题的关键是能够根据经过的点的坐标确定反比例函数的比例系数,难度不大.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
16.若分式方程$\frac{x+2a}{x(x-1)}$-$\frac{5}{x}$=$\frac{6}{x-1}$有增根,则a的值为( )
| A. | 1 | B. | 2.5 | C. | -2.5或2.5 | D. | 0或1 |
17.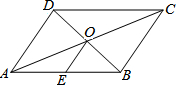 如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
 如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
12. 如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是( )
如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是( )
 如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是( )
如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是( )| A. | 70° | B. | 31° | C. | 79° | D. | 90° |
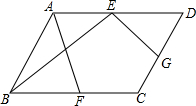 在平行四边形ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,则AF的长为4.
在平行四边形ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2$\sqrt{5}$,AB=3,则AF的长为4. 如图所示,直线AB∥CD,∠1=80°,求∠2的度数.
如图所示,直线AB∥CD,∠1=80°,求∠2的度数.