题目内容
14.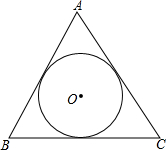 如图,△ABC的周长为24,面积为24,求它的内切圆的半径.
如图,△ABC的周长为24,面积为24,求它的内切圆的半径.
分析 连结OA、OB、OC,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,根据切线的性质得OD=OE=OF=r,则利用S△ABC=S△AOB+S△OBC+S△OAC得到$\frac{1}{2}$•r•AB+$\frac{1}{2}$•r•BC+$\frac{1}{2}$•r•AC=24,变形得到$\frac{1}{2}$r(AB+BC+AC)=24,然后把周长为24代入计算即可得到r的值.
解答 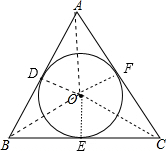 解:连结OA、OB、OC,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,
解:连结OA、OB、OC,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,
设它的内切圆的半径为r,则OD=OE=OF=r,
∵S△ABC=S△AOB+S△OBC+S△OAC,
∴$\frac{1}{2}$•r•AB+$\frac{1}{2}$•r•BC+$\frac{1}{2}$•r•AC=24,
∴$\frac{1}{2}$r(AB+BC+AC)=24,
∴$\frac{1}{2}$r•24=24,
∴r=2.
即它的内切圆的半径为2.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点,三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
6.反比例函数y=$\frac{a}{x}$的图象与二次函数y=ax2+bx+c的图象的交点,最多有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
11. 如图,?ABCD中,E为AD中点,已知△DEF的面积为S,则?ABCD面积为( )
如图,?ABCD中,E为AD中点,已知△DEF的面积为S,则?ABCD面积为( )
 如图,?ABCD中,E为AD中点,已知△DEF的面积为S,则?ABCD面积为( )
如图,?ABCD中,E为AD中点,已知△DEF的面积为S,则?ABCD面积为( )| A. | 4s | B. | 6s | C. | 12s | D. | 10s |
 已知:如图,Rt△ABC中,∠ACB=90°°,AC=3,BC=4.
已知:如图,Rt△ABC中,∠ACB=90°°,AC=3,BC=4. 如图所示,在△ABC中,AB=5,AC=13,BC边上的中线AD=6.求BC2.
如图所示,在△ABC中,AB=5,AC=13,BC边上的中线AD=6.求BC2.