题目内容
11．
如图，?ABCD中，E为AD中点，已知△DEF的面积为S，则?ABCD面积为（ ）| A． | 4s | B． | 6s | C． | 12s | D． | 10s |
分析 由于四边形ABCD是平行四边形，那么AD∥BC，AD=BC，根据平行线分线段成比例定理的推论可得△DEF∽△BCF，再根据E是AD中点，易求出相似比，从而可求△BCF的面积，再利用△BCF与△DEF是同高的三角形，则两个三角形面积比等于它们的底之比，从而易求△DCF的面积，进而可求?ABCD的面积．
解答 解：如图所示，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴△DEF∽△BCF，
∴S△DEF：S△BCF=（$\frac{DE}{BC}$）2，
又∵E是AD中点，
∴DE=$\frac{1}{2}$AD=$\frac{1}{2}$BC，
∴DE：BC=DF：BF=1：2，
∴S△DEF：S△BCF=1：4，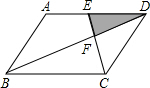
∴S△BCF=4S，
又∵DF：BF=1：2，
∴S△DCF=2S，
∴S?ABFE=2（S△DCF+S△BCF）=2（2S+4S）=12S．
故选：C．
点评 本题考查了平行四边形的性质、平行线分线段成比例定理的推论、相似三角形的判定和性质．解题的关键是知道相似三角形的面积比等于相似比的平方、同高两个三角形面积比等于底之比，先求出△BCF的面积．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
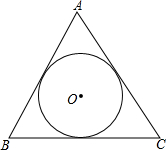如图，△ABC的周长为24，面积为24，求它的内切圆的半径．
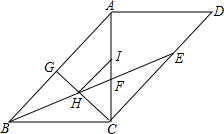如图，平行四边形ABCD中，对角线AC⊥BC，BE平分∠ABC，交CD于点E，且与AC交于点F．过点C作CG1AB于点G，CG与BE交于点H，点I在线段AC上，且HI∥AB．求证：
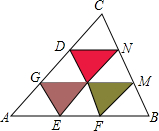如图，在△ABC中，AB=30，BC=24，CA=27，AE=EF=FB，EG∥FD∥BC，FM∥EN∥AC，则图中阴影部分的三个三角形的周长之和为（ ）
20．用四舍五入法按要求对1.5268分别取近似值，其中错误的是（ ）
| A． | 1.5（精确到0.1） | B． | 1.5（精确到个位） | ||
| C． | 1.53（保留三个有效数字） | D． | 1.53（精确到0.01） |