题目内容
8.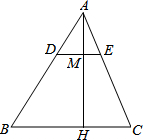 如图所示:AH是△ABC的边上的高,M为AH上一点,且AM:MH=1:2,过M引DE∥BC分别交AB,AC于点D,E,若BC=16cm、AH=9cm.
如图所示:AH是△ABC的边上的高,M为AH上一点,且AM:MH=1:2,过M引DE∥BC分别交AB,AC于点D,E,若BC=16cm、AH=9cm.(1)求△ADE的面积;
(2)AM:MH为何值时,S△ADE:S平行四边形BDEC=1:1?
分析 (1)根据DE∥BC,AH是△ABC的边上的高,得到AM⊥DE,由于AM:MH=1:2,推出AM:AH=1:3,通过△ADE∽△ABC,得到$\frac{DE}{BC}=\frac{AM}{AH}$=$\frac{1}{3}$,于是得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=$\frac{1}{9}$,即可得到结果;
(2)由S△ADE:S平行四边形BDEC=1:1,得到S△ADE:S△ABC=1:2,根据相似三角形的性质得到AM:AH=$\sqrt{2}$:2,即可得到结论.
解答 解:(1)∵DE∥BC,AH是△ABC的边上的高,
∴AM⊥DE,
∵AM:MH=1:2,
∴AM:AH=1:3,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AM}{AH}$=$\frac{1}{3}$,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=$\frac{1}{9}$,
∵S△ABC=$\frac{1}{2}$BC•AH=$\frac{1}{2}×16×9$=72,
∴△ADE的面积=8;
(2)∵S△ADE:S平行四边形BDEC=1:1,
∴S△ADE:S△ABC=1:2,
由(1)证得△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=($\frac{AM}{AH}$)2=$\frac{1}{2}$,
∴AM:AH=$\sqrt{2}$:2,
∴AM:MH=$\sqrt{2}$:(2-$\sqrt{2}$).
∴当AM:MH=$\sqrt{2}$:(2-$\sqrt{2}$)时,S△ADE:S四边形BDEC=1:1.
点评 本题考查了相似三角形的判定和性质,三角形的面积,熟练掌握相似三角形的判定和性质是解题的关键.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在同一直线上,再添加一个下列条件,不能判断△ABC≌△EDF的是( )
如图,在△ABC与△EDF中,∠B=∠D=90°,∠A=∠E,B、F、C、D在同一直线上,再添加一个下列条件,不能判断△ABC≌△EDF的是( )| A. | AB=ED | B. | AC=EF | C. | AC∥EF | D. | BC=DF |
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
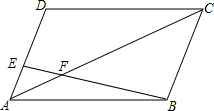 如图,平行四边形ABCD中,AE:ED=1:2,S△AEF=6cm2,则S△CBF等于54cm2.
如图,平行四边形ABCD中,AE:ED=1:2,S△AEF=6cm2,则S△CBF等于54cm2.