题目内容
19.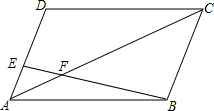 如图,平行四边形ABCD中,AE:ED=1:2,S△AEF=6cm2,则S△CBF等于54cm2.
如图,平行四边形ABCD中,AE:ED=1:2,S△AEF=6cm2,则S△CBF等于54cm2.
分析 根据相似三角形的性质,可得△AEF∽△CBF,由已知可证$\frac{{S}_{△AEF}}{{S}_{△CBF}}$=($\frac{AE}{BC}$)2=$\frac{1}{9}$,继而求得S△CBF=9S△AEF=54cm2.
解答 解:∵AE:ED=1:2,
$\frac{AE}{AD}$=$\frac{1}{3}$,
∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{{S}_{△AEF}}{{S}_{△CBF}}$=($\frac{AE}{BC}$)2=$\frac{1}{9}$,
∴S△CBF=9S△AEF=54cm2.
故答案为:54cm2.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△AEF∽△CBF是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
10.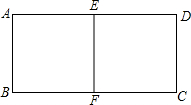 如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )
如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )
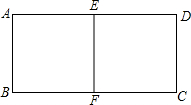 如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )
如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )| A. | 2:1 | B. | 3:1 | C. | $\sqrt{2}$:1 | D. | 4:1 |
7.下列命题中,正确的是( )
| A. | 全等的图形一定是位似图形 | B. | 相似的图形一定是位似图形 | ||
| C. | 位似图形一定是全等图形 | D. | 位似图形一定是相似图形 |
9.若3m=5,9n=10,则18m+18n=( )
| A. | 50 | B. | 500 | C. | 250 | D. | 2500 |
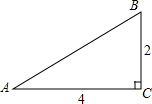 如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,求∠A,∠B及AB的长.
如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,求∠A,∠B及AB的长.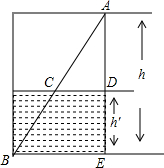 如图,一油桶高1m,桶内有油,一根木棒长1.2m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48m,求桶内油面的高度.
如图,一油桶高1m,桶内有油,一根木棒长1.2m,从桶盖的小口处斜插入桶内,一端插到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长为0.48m,求桶内油面的高度.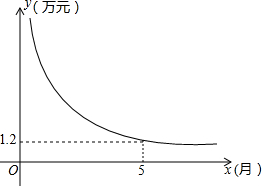 黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动,她购买的别克汽车价格为16.3万元,交了首付之后每月付款y万元,x月结清余款,y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.
黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动,她购买的别克汽车价格为16.3万元,交了首付之后每月付款y万元,x月结清余款,y与x的函数关系如图所示,试根据图象提供的信息回答下列问题.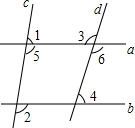 如图,∠1+∠2=180°,∠3=108°,求∠4的度数的过程填写完整.
如图,∠1+∠2=180°,∠3=108°,求∠4的度数的过程填写完整.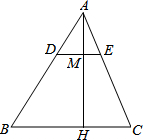 如图所示:AH是△ABC的边上的高,M为AH上一点,且AM:MH=1:2,过M引DE∥BC分别交AB,AC于点D,E,若BC=16cm、AH=9cm.
如图所示:AH是△ABC的边上的高,M为AH上一点,且AM:MH=1:2,过M引DE∥BC分别交AB,AC于点D,E,若BC=16cm、AH=9cm.