题目内容
18.在△ABC中,∠B=90°,sinA=$\frac{\sqrt{3}}{4}$,BC=2$\sqrt{3}$,则AB=8.分析 根据锐角的正弦为对边比斜边,可得答案.
解答 解:在△ABC中,∠B=90°,sinA=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{4}$,
AB=BC÷$\frac{\sqrt{3}}{4}$=2$\sqrt{3}$×$\frac{4}{\sqrt{3}}$=8,
故答案为:8.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
3.在△ABC中,∠C=90°,AC=3BC,则sinA=$\frac{\sqrt{10}}{10}$,cosA=$\frac{3\sqrt{10}}{10}$,tanA=$\frac{1}{3}$.
10.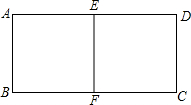 如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )
如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )
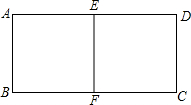 如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )
如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为( )| A. | 2:1 | B. | 3:1 | C. | $\sqrt{2}$:1 | D. | 4:1 |
7.下列命题中,正确的是( )
| A. | 全等的图形一定是位似图形 | B. | 相似的图形一定是位似图形 | ||
| C. | 位似图形一定是全等图形 | D. | 位似图形一定是相似图形 |
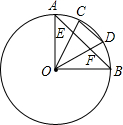 如图,在⊙O中半径OA⊥OB,C,D是$\widehat{AB}$的两个三等分点,弦AB分别交OC,OD于E,F点.求证:AE=BF=CD.(提示:连接AC,BD,先证:AC=CD=BD)
如图,在⊙O中半径OA⊥OB,C,D是$\widehat{AB}$的两个三等分点,弦AB分别交OC,OD于E,F点.求证:AE=BF=CD.(提示:连接AC,BD,先证:AC=CD=BD)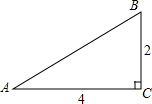 如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,求∠A,∠B及AB的长.
如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,求∠A,∠B及AB的长. 地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄在北偏西52°方向.
地震发生后,一支专业搜救队驱车前往灾区救援.如图,汽车在一条南北走向的公路上向北行驶,当在A处时,车载GPS(全球卫星定位系统)显示村庄C在北偏西26°方向,汽车以35km/h的速度前行2h到达B处,GPS显示村庄在北偏西52°方向. 如图①、②分别表示甲、乙两个楼梯.
如图①、②分别表示甲、乙两个楼梯.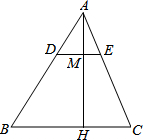 如图所示:AH是△ABC的边上的高,M为AH上一点,且AM:MH=1:2,过M引DE∥BC分别交AB,AC于点D,E,若BC=16cm、AH=9cm.
如图所示:AH是△ABC的边上的高,M为AH上一点,且AM:MH=1:2,过M引DE∥BC分别交AB,AC于点D,E,若BC=16cm、AH=9cm.