题目内容

17．先化简，再求值：$\frac{x-3}{2x-4}$÷（$\frac{5}{x-2}$-x-2），其中x=$\sqrt{3}$-3．

分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．

解答 解：原式=$\frac{x-3}{2（x-2）}$÷$\frac{5-（x+2）（x-2）}{x-2}$=$\frac{x-3}{2（x-2）}$•$\frac{x-2}{-（x+3）（x-3）}$=-$\frac{1}{2（x+3）}$，
当x=$\sqrt{3}$-3时，原式=-$\frac{\sqrt{3}}{6}$．

点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
7．下列命题中，正确的是（　　）
A．全等的图形一定是位似图形B．相似的图形一定是位似图形
C．位似图形一定是全等图形D．位似图形一定是相似图形
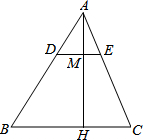8．如图所示：AH是△ABC的边上的高，M为AH上一点，且AM：MH=1：2，过M引DE∥BC分别交AB，AC于点D，E，若BC=16cm、AH=9cm．
（1）求△ADE的面积；
（2）AM：MH为何值时，S△ADE：S平行四边形BDEC=1：1？
5．计算
（1）（3.14-π）0-2-3+（-4）2÷（$\frac{1}{2}$）-2
（2）（-3x）3+（x4）2÷（-x）5．
12．当x-$\frac{3}{2}$≤x＜-1或x＞-1 时，$\sqrt{2x+3}$+$\frac{1}{x+1}$在实数范围内有意义．
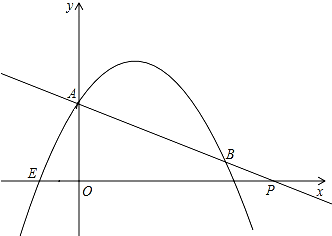2．如图，在平面直角坐标系中，抛物线y=-$\frac{1}{2}$x2+bx+c的图象过点E（-1，0）、点A（0，2）两点．
（1）求抛物线的解析式（关系式）；
（2）直线y=-$\frac{1}{3}$x+2交x轴于点P，交y轴于点A．并与抛物线相交于A、B两点．
①在x轴的正半轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由；
②若抛物线与坐标轴的另一个交点为F，将线段EF在x轴上平移，当线段EF怎样平移时，四边形ABFE的周长最小？求出此时点E、F的坐标．
9．若3m=5，9n=10，则18m+18n=（　　）
A．50B．500C．250D．2500
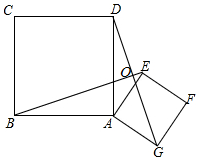8．如图，已知正方形ABCD和正方形AEFG，连结BE、DG．
（1）求证：BE=DG，BE⊥DG；
（2）连接BD、EG、DE，点M、N、P分别是BD、EG、DE的中点，连接MP，PN，MN，求证：△MPN是等腰直角三角形；
（3）若AB=4，EF=2$\sqrt{2}$，∠DAE=45°，直接写出MN=2$\sqrt{5}$．
9．下列因式分解中错误的是（　　）
A．-mx-my=-m（x+y）B．a2-a-$\frac{1}{4}$=（a-$\frac{1}{2}$）2
C．1-9a2=（1+3a）（1-3a）D．$\frac{1}{4}$a2b2-1=（$\frac{1}{2}$ab+1）（$\frac{1}{2}$ab-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网