题目内容
19.阅读材料:为解方程(x2-3)2-5(x2-3)+4=0,我们可以将x2-3看作一个整体,然后设x2-3=y,则原方程可化为y2-5y+4=0,(1)
从而解得y1=1,y2=4.
当y1=1时,x2-3=1解得x1=2,x2=-2
当y2=4时,x2-3=4解得x3=$\sqrt{7}$,x4=-$\sqrt{7}$,
∴原方程的解为x1=2,x2=-2,x3=$\sqrt{7}$,x4=-$\sqrt{7}$.
解答问题:
(1)填空:在原方程得到方程(1)的过程中,利用换元法达到降次的目的,体现了转化的数学思想.
(2)解方程x4-8x2+12=0.
分析 (1)根据换元法解一元二次方程的过程及意义,即可得出结论;
(2)设x2=y,则原方程可化为y2-8y+12=0,解方程求出y值,进而得出x的值.
解答 解:(1)在原方程得到方程y2-5y+4=0的过程中,利用了换元法达到了降次的目的,体现了转化的数学思想.
故答案为:换元,转化;
(2)设x2=y,则原方程可化为y2-8y+12=0,
解之得:y1=2,y2=6,
当 y=2 时,x2=2,
解得:x1=$\sqrt{2}$,x2=-$\sqrt{2}$;
当 y=6 时,x2=6,
解得:x3=$\sqrt{6}$,x4=-$\sqrt{6}$.
∴原方程的解为x1=$\sqrt{2}$,x2=-$\sqrt{2}$,x3=$\sqrt{6}$,x4=-$\sqrt{6}$.
点评 本题考查了换元法解一元二次方程,熟练掌握利用换元法解一元二次方程的方法是解题的关键.

练习册系列答案
相关题目
7.若(x-1)2-1=0,则x的值为( )
| A. | ±1 | B. | ±2 | C. | -2或0 | D. | 0或2 |
14.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则下列条件不能判定△ABC是直角三角形的是( )
| A. | ∠A=∠B-∠C | B. | ∠A:∠B:∠C=1:3:4 | C. | $a:b:c=1:\sqrt{2}:3$ | D. | a2+c2=b2 |
11.下列选项中,正确的是( )
| A. | -(x-y)=-x-y | B. | 若3x=4y,则3x+5m=4y+5m | ||
| C. | 若am2=bm2,则a=b | D. | 1÷($\frac{1}{3}$-$\frac{1}{2}$)=1÷$\frac{1}{3}$-1÷$\frac{1}{2}$=3-2=1 |
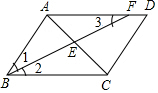 如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.若AB=3,BC=5,求$\frac{AE}{AC}$的值.
如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.若AB=3,BC=5,求$\frac{AE}{AC}$的值.