题目内容
13.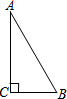 △ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按$\sqrt{3}$:1放大,A、B的对应点分别为A′、B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为4或2.
△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按$\sqrt{3}$:1放大,A、B的对应点分别为A′、B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为4或2.
分析 利用直角三角形中30°所对的边与斜边的关系以及勾股定理得出AC,BC的长,再利用位似图形的性质得出A′C,CB′的长,再利用旋转的性质得出答案.
解答 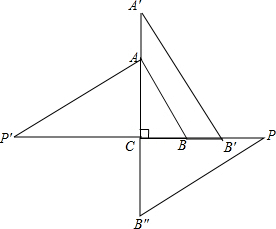 解:如图所示:∵∠C=90°,∠A=30°,AB=2,
解:如图所示:∵∠C=90°,∠A=30°,AB=2,
∴BC=1,AC=$\sqrt{3}$,
∵以点C为位似中心将△ABC按$\sqrt{3}$:1放大,
∴CB′=$\sqrt{3}$,A′C=3,
当将△A′B′C绕点C顺时针旋转90°,
则PB=PC-BC=3-1=2,
当将△A′B′C绕点C逆时针旋转90°,
则P′B=P′C+BC=3+1=4,
综上所述:点P与B之间的距离为4或2.
故答案为:4或2.
点评 此题主要考查了位似变换以及旋转变换、勾股定理等知识,正确进行分类讨论得出是解题关键.

练习册系列答案
相关题目
18.下列正多边形中,不能够铺满地面的是( )
| A. | 等边三角形 | B. | 正方形 | C. | 正六边形 | D. | 正八边形 |
 如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动.3秒后,两点相距12个单位长度.已知动点A、B的速度比是1:3(速度单位:1个单位长度/秒).
如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动.3秒后,两点相距12个单位长度.已知动点A、B的速度比是1:3(速度单位:1个单位长度/秒). 如图,点M是线段AB的中点,N在MB上,MN=$\frac{2}{5}$AM,若AM=15cm.求线段NB的长.
如图,点M是线段AB的中点,N在MB上,MN=$\frac{2}{5}$AM,若AM=15cm.求线段NB的长.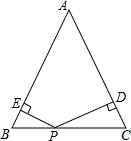 如图,△ABC中,AB=AC=4,P是BC上任意一点,过P作PD⊥AC于D,PE⊥AB于E,若S△ABC=6,则PE+PD=3.
如图,△ABC中,AB=AC=4,P是BC上任意一点,过P作PD⊥AC于D,PE⊥AB于E,若S△ABC=6,则PE+PD=3.