题目内容
12.在直角坐标系中,O为坐标原点,设点P(1,m)在函数$y=\frac{{\sqrt{3}}}{x}$的图象上,以OP为边作正方形OPQR,则OP=2;若反比例函数$y=\frac{k}{x}$经过点Q,则k=2或-2.分析 把P(1,m)代入$y=\frac{{\sqrt{3}}}{x}$即可求得m的值,然后根据勾股定理求得OP的长,作PM⊥x轴于M,QN⊥PM于N,通过证得△POM≌△QPN,得出PN=OM=1,NQ=PM=$\sqrt{3}$,从而求得Q的坐标,把Q点的坐标代入$y=\frac{k}{x}$即可求得k的值.
解答  解:∵点P(1,m)在函数$y=\frac{{\sqrt{3}}}{x}$的图象上,
解:∵点P(1,m)在函数$y=\frac{{\sqrt{3}}}{x}$的图象上,
∴m=$\sqrt{3}$,
∴P(1,$\sqrt{3}$),
∴OP=$\sqrt{{1}^{2}+({\sqrt{3})}^{2}}$=2,
如图,作PM⊥x轴于M,QN⊥PM于N,
∵OM=1,PM=$\sqrt{3}$,
∴tan∠POM=$\frac{PM}{OM}$=$\sqrt{3}$,
∴∠POM=60°,
∴∠OPM=30°
∴∠QPN=90°-30°=60°,
∴∠POM=∠QPN,
在△POM和△QPN中,
$\left\{\begin{array}{l}{∠POM=∠QPN}\\{∠PMO=∠QNP=90°}\\{OP=PQ}\end{array}\right.$
∴△POM≌△QPN,
∴PN=OM=1,NQ=PM=$\sqrt{3}$,
∴Q1(1+$\sqrt{3}$,$\sqrt{3}$-1),
同理证得Q2(1-$\sqrt{3}$,1+$\sqrt{3}$),
∴k=(1+$\sqrt{3}$)×($\sqrt{3}$-1)=2,或k=(1+$\sqrt{3}$)(1-$\sqrt{3}$)=-2,
故答案为2,2或-2.
点评 本题考查了反比例函数图象上点的坐标特征,勾股定理的应用,求得Q点的坐标是解题的关键.

练习册系列答案
相关题目
2.计算(2a2b)2的正确结果是( )
| A. | 4a2b | B. | 2a4b2 | C. | 4a4b2 | D. | 2a4b |
3.京沪高速公路济南至莱芜段全长120千米,一辆小汽车和一辆客车同时从济南、莱芜两地相向开出,经过50分钟相遇,小汽车比客车多行驶20千米.设小汽车和客车的平均速度为x千米/小时,y千米/小时,则下列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x-y=20}\\{50x+50y=120}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=20}\\{\frac{5}{6}x+50y=120}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{50x-50y=20}\\{50x+50y=120}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{5}{6}x-\frac{5}{6}y=20}\\{\frac{5}{6}x+\frac{5}{6}y=120}\end{array}\right.$ |
 如图,已知BC⊥CD,∠1=∠2=∠3.
如图,已知BC⊥CD,∠1=∠2=∠3.
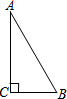 △ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按$\sqrt{3}$:1放大,A、B的对应点分别为A′、B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为4或2.
△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按$\sqrt{3}$:1放大,A、B的对应点分别为A′、B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为4或2.