题目内容
1.已知抛物线C1:y=x2-4x+3与x轴交于A、B两点,与y轴交于C点,点P在对称轴上.点Q在第一象限的抛物线上,且以B、C、P为顶点三角形与以B、C、Q为顶点三角形全等.求Q点坐标.分析 根据抛物线解析式求出A、B、C三点的坐标,观察P、B两点坐标,可以得出两点纵坐标差1,且P、Q两点关于直线BC对称,根据直线解析式设出点Q的坐标,将Q坐标带入抛物线解析式即可求出点Q坐标.
解答 解:∵y=x2-4x+3=(x-3)(x-1)
∴y=0时,可得x1=1,x2=3;x=0时,y=3;对称轴为:x=$-\frac{-4}{2×1}=2$
∴点A的坐标为(1,0),点B的坐标为(3,0),点C的坐标为(0,3)
∵点P在对称轴上,点Q在第一象限的抛物线上,设点P的坐标为(2,y),点Q的坐标为(x,x2-4x+3),
∴P、B两点横坐标差1,
∵以B、C、P为顶点三角形与以B、C、Q为顶点三角形全等,
∴点Q纵坐标为1,且点P、Q关于直线BC对称,
∴设直线PQ解析式为y=kx+b,
当y=1,x=1-b,
∵点Q在抛物线上,
∴1=(1-b)2-4(1-b)+3,
解得:b=-1-$\sqrt{2}$,或b=-1+$\sqrt{2}$,
∵b<0,
∴b=-1-$\sqrt{2}$,
∴直线PQ解析式为:y=x-1-$\sqrt{2}$,
当x=2时,y=1-$\sqrt{2}$,
∴点P坐标为(2,1-$\sqrt{2}$).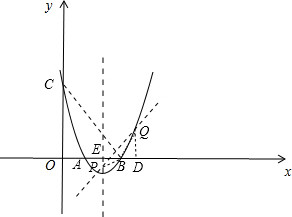
点评 本题考查了二次函数的综合应用,题目以二次函数为框架,考察全等三角形,一次函数的性质等知识点,题目的关键是根据全等三角形找出点Q的坐标特征,进而求出点Q的坐标.题目整体设计较难,考查学生的解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列说法错误的是( )
| A. | 27的立方根是3 | B. | (-1)2016是最小的正整数 | ||
| C. | 两个无理数的和一定是无理数 | D. | 实数与数轴上的点一一对应 |

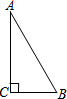 △ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按$\sqrt{3}$:1放大,A、B的对应点分别为A′、B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为4或2.
△ABC中,∠C=90°,∠A=30°,AB=2.以点C为位似中心将△ABC按$\sqrt{3}$:1放大,A、B的对应点分别为A′、B′,再将△A′B′C绕点C旋转90°,A′的对应点为P,则点P与B之间的距离为4或2.