Question

3．在平面直角坐标系中，一次函数y=kx+4m（m＞0）的图象经过点B（p，2m），其中m＞0．
（1）若m=1，且k=-1，求点B的坐标；
（2）已知点A（m，0），若直线y=kx+4m与x轴交于点C（n，0），n+2p=4m，试判断线段AB上是否存在一点N，使得点N到坐标原点O与到点C的距离之和等于线段OB的长，并说明理由．

Answer 1

分析 （1）根据待定系数法解答即可；
（2）用待定系数法确定函数的解析式，再根据勾股定理解答即可．

解答 解：（1）∵一次函数y=kx+4m（m＞0）的图象经过点B（p，2m），
∴2m=kp+4m．
∴kp=-2m．
∵m=1，k=-1，
∴p=2．
∴B（2，2）．
（2）线段AB上存在一点N，使得点N到坐标原点O与到点C的距离之和等于线段OB的长．
理由如下：
由题意，将B（p，2m），C（n，0）分别代入y=kx+4m，
得kp+4m=2m且kn+4m=0．
可得n=2p．
∵n+2p=4m，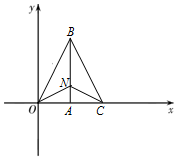

∴p=m．
∴A（m，0），B（m，2m），C（2m，0）．
∵x_B=x_A，
∴AB⊥x轴，
且  OA=AC=m．
∴对于线段AB上的点N，有NO=NC．
∴点N到坐标原点O与到点C的距离之和为NO+NC=2NO．
∵∠BAO=90°，
在Rt△BAO，Rt△NAO中分别有
OB²=AB²+OA²=5m²，NO²=NA²+OA²=NA²+m²．
若2NO=OB，
则4NO²=OB²．
即4（NA²+m²）=5m²．
可得NA=$\frac{1}{2}$m．
即NA=$\frac{1}{4}$AB．
所以线段AB上存在一点N，使得点N到坐标原点O与到点C的距离之和等于线段OB的长，且NA=$\frac{1}{4}$AB．

点评 此题考查点的坐标与解析式的关系以及待定系数法的应用，用待定系数法确定函数的解析式，是常用的一种解题方法．同学们要熟练掌握这种方法．