题目内容
8. 用一元一次方程的知识解决下面的问题:
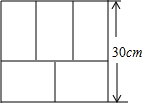
用一元一次方程的知识解决下面的问题:(1)如图,工人师傅用5块相同的长方形地砖铺成了一个大长方形,求每块小长方形地砖的长和宽各是多少?
(2)小明和小亮约好上午8点分别从A、B两地同时出发,相向而行,则上午10点两人相距18km,中午12点两人又相距18km.已知小明每小时比小亮多走2km.请根据以上信息解答下列问题:
①小明和小亮的速度各是多少?
②A、B两地的距离是多少?
分析 (1)设每块小长方形地砖的长是xcm,则宽为(30-x)cm,利用“3个小矩形的宽=2个小矩形的长”列出方程并解答即可;
(2)①设小亮的速度是每小时xkm,则小明的速度是每小时(x+2)km,由两人的路程之和为36km建立方程求出其解即可.
解答 解:(1)设每块小长方形地砖的长是xcm,则宽为(30-x)cm,由题意得
3(30-x)=2x,
解得x=18,
30-x=12.
答:每块小长方形地砖的长是18cm,则宽为12cm;
(2)①设小亮的速度是每小时xkm,则小明的速度是每小时(x+2)km,
由题意得:2x+2(x+2)=18×2,
解得,x=8,
x+2=10(km).
所以,小亮的速度是每小时8km,则小明的速度是每小时10km;
②由题意知,A、B两地的距离是:2(8+10)+18=54(km).
点评 本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,行程问题的数量关系的运用,解答时由两人的路程之和为36km建立方程是关键.

练习册系列答案
相关题目
18.某商场试销一种商品,成本为每件100元,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如下表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
| 销售单价x(元) | … | 130 | 135 | 140 | 145 | … |
| 销售量y(件) | … | 240 | 230 | 220 | 210 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
16.在平面直角坐标系中,点(2,-3)关于原点对称的点的坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (-2,-3) | D. | (3,-2) |
13. 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
 如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
20.方程3x2-8x-10=0的二次项系数和一次项系数分别为( )
| A. | 3和8 | B. | 3和-8 | C. | 3和-10 | D. | 3和10 |
17.下列计算正确的是( )
| A. | 3a+2b=5ab | B. | 5y-3y=2 | C. | 3x2y-2yx2=x2y | D. | -3x+5x=-8x |
18.已知a=25000用科学记数法表示为2.5×4,那么a2用科学记数法表示为( )
| A. | 62.5×108 | B. | 6.25×109 | C. | 6.25×108 | D. | 6.25×107 |