题目内容
15.已知抛物线y=mx2+(m+3)x+3的顶点在x轴上,求m的值.分析 由顶点在x轴上可知方程mx2+(m+3)x+3=0有两个相等的实数根,再利用判别式为0可得到关于m的方程,可求得m的值.
解答 解:
∵y=mx2+(m+3)x+3的顶点在x轴上,
∴方程mx2+(m+3)x+3=0有两个相等的实数根,
∴△=0,即(m+3)2-12m=0,解得m=3.
点评 本题主要考查二次函数的性质,掌握二次函数与一元二次方程的关系是解题的关键.

练习册系列答案
相关题目
5. 如图,南偏东15°和北偏东25°的两条射线组成的角(即∠AOB)等于( )
如图,南偏东15°和北偏东25°的两条射线组成的角(即∠AOB)等于( )
 如图,南偏东15°和北偏东25°的两条射线组成的角(即∠AOB)等于( )
如图,南偏东15°和北偏东25°的两条射线组成的角(即∠AOB)等于( )| A. | 40° | B. | 80° | C. | 140° | D. | 150° |
20.方程3x2-8x-10=0的二次项系数和一次项系数分别为( )
| A. | 3和8 | B. | 3和-8 | C. | 3和-10 | D. | 3和10 |
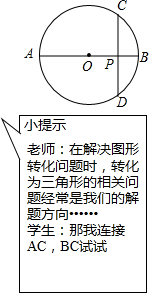 如图,CD是圆O的弦,AB是直径,且CD⊥AB,垂足为P.
如图,CD是圆O的弦,AB是直径,且CD⊥AB,垂足为P. 已知:线段a,b
已知:线段a,b
 如图,有一半圆形桥拱,拱的跨度AB=40米,那么桥拱的弧长为62.8米.(结果精确到0.1米)
如图,有一半圆形桥拱,拱的跨度AB=40米,那么桥拱的弧长为62.8米.(结果精确到0.1米)