题目内容
14.等腰三角形腰长为6,一腰上的中线将其周长分成两部分的差为2,则这个等腰三角形的周长为( )| A. | 14 | B. | 16或20 | C. | 16 | D. | 14或22 |
分析 先根据题意画出图形,设AE为底边上的高,由D为AC中点,得到AD=DC,再根据BD将其周长分成两部分的差为2,分别表示出BD分三角形周长的两部分,相减等于3列出关于BC的方程,求出方程的解得到BC的长.
解答 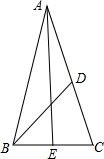 解:如图所示,AB=AC=6,D为AC中点,AE⊥BC于E.
解:如图所示,AB=AC=6,D为AC中点,AE⊥BC于E.
∵D为AC的中点,
∴AD=DC=2,
根据题意得:(AB+AD)-(CB+CD)=2或(CB+CD)-(AB+AD)=2,
即(6+2)-(CB+2)=2或(CB+2)-(6+2)=2,
解得:BC=4或8,
故周长为16或20,
故选B.
点评 此题考查了等腰三角形的性质,以及勾股定理,要求学生借助图形,采用数形结合及分类讨论的思想,求出底边BC的长,同时注意因为没有指明周长分成两部分的长短,故BC求出有两解,不要遗漏.

练习册系列答案
相关题目
2.不等式组$\left\{\begin{array}{l}{3-x≤5}\\{\frac{1}{2}(x+1)<1}\end{array}\right.$的解集在数轴上可表示为( )
| A. | 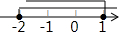 | B. | 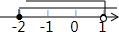 | C. |  | D. |  |
19.用放大镜观察一个三角形时,不变的量是( )
| A. | 各条边的长度 | B. | 各个角的度数 | C. | 三角形的面积 | D. | 三角形的周长 |
6.下列计算正确的是( )
| A. | a10-a7=a3 | B. | (-2a2b)2=-2a4b2 | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | (a+b)9÷(a+b)3=(a+b)6 |
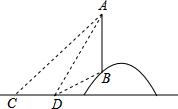 如图,一电线杆AB立在山坡上,从地面的点C看,测得杆顶端点A的仰角为45°向前走6m到达点D,又测得杆顶端点A和杆底端点B的仰角分别是60°和30°.
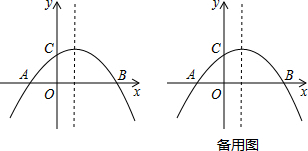
如图,一电线杆AB立在山坡上,从地面的点C看,测得杆顶端点A的仰角为45°向前走6m到达点D,又测得杆顶端点A和杆底端点B的仰角分别是60°和30°. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.