题目内容
4.已知在一个不透明的口袋里装有形状、大小相同的红球4个、绿球5个和黄球若干个,任意摸出一个球是绿色的概率是$\frac{1}{3}$,那么口袋里黄球的个数为6.分析 根据概率的意义:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$,可得答案.
解答 解:设绿色球有x个,
由形状、大小相同的红球4个、绿球5个和黄球若干个,任意摸出一个球是绿色的概率是$\frac{1}{3}$,得
$\frac{5}{4+5+x}$=$\frac{1}{3}$,
解得x=6,
故答案为:6.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目
15. 如图,数轴上的A,B,C,D四点中,与表示-$\sqrt{7}$的点最接近的是( )
如图,数轴上的A,B,C,D四点中,与表示-$\sqrt{7}$的点最接近的是( )
 如图,数轴上的A,B,C,D四点中,与表示-$\sqrt{7}$的点最接近的是( )
如图,数轴上的A,B,C,D四点中,与表示-$\sqrt{7}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
12.平面直角坐标系中有一点P,点P到y轴的距离为2,点P的纵坐标为-3,则点P的坐标是( )
| A. | (-3,-2) | B. | (-2,-3) | C. | (2,-3) | D. | (2,-3)或(-2,-3) |
16.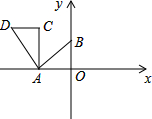 如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )
如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )
 如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )
如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )| A. | (4,3) | B. | (-3,4) | C. | (-7,4) | D. | (-7,3) |
13. 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )
 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )| A. | 3cm | B. | 3.5cm | C. | 4cm | D. | 4.5cm |
14.等腰三角形腰长为6,一腰上的中线将其周长分成两部分的差为2,则这个等腰三角形的周长为( )
| A. | 14 | B. | 16或20 | C. | 16 | D. | 14或22 |
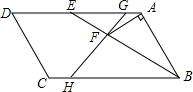 如图,?ABCD中,BE平分∠ABC,交AD于点E,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,且AB=6,则BH=10;△AFG的面积=$\frac{{\sqrt{3}}}{2}$.
如图,?ABCD中,BE平分∠ABC,交AD于点E,AF⊥AB,交线段BE于点F,G为AE上一点,AG:GE=1:5,连结GF并延长交边BC于点H.若GE:BH=1:2,且AB=6,则BH=10;△AFG的面积=$\frac{{\sqrt{3}}}{2}$.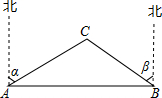 如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.
如图,已知A、B两市相距150千米,分别从A、B处测得某风景区中心C处的方向角如图所示,风景区区域是以C为圆心,52千米为半径的圆,tanα≈1.63,tanβ≈1.37.有关部门要设计修建连接AB两市的高速公路,问连接AB的高速公路是否穿过风景区,请说明理由.