题目内容
11.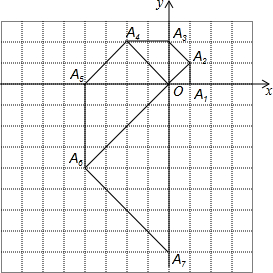 如图,O为坐标原点,点A1坐标为(1,0),以OA1为直角边作等腰直角△OA1A2,以OA2为直角边作等腰直角△OA2A3,以OA3为直角边作等腰直角△OA3A4,…,依此法继续作下去,OA2015=21007.
如图,O为坐标原点,点A1坐标为(1,0),以OA1为直角边作等腰直角△OA1A2,以OA2为直角边作等腰直角△OA2A3,以OA3为直角边作等腰直角△OA3A4,…,依此法继续作下去,OA2015=21007.
分析 如图,首先求出OA1、OA2、OA3、OA4,由此观察、比较、分析、猜测所得到的四个数之间的比值关系,进而求出OA2015,即可解决问题.
解答  解:如图,由题意得:OA1=$\sqrt{1}$,OA2=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
解:如图,由题意得:OA1=$\sqrt{1}$,OA2=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
OA3=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=$\sqrt{4}$,OA4=$\sqrt{4+4}=\sqrt{8}$,
OA5=$\sqrt{16}$,由此可以发现:根号内的数,比值不变,
∴可以猜想:OA2015=$\sqrt{1×{2}^{2014}}$=21007,
故答案为21007.
点评 该题主要考查了勾股定理、等腰直角三角形的性质等知识点及其应用问题;解题的关键是数形结合,经过观察分析,正确找出相邻线段之间的比值关系.对观察、比较、分析、猜想等能力提出了一定的要求.

练习册系列答案
相关题目
1.已知a,b都是整数,且满足a2+b2+1<2a-2b,则a+b=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.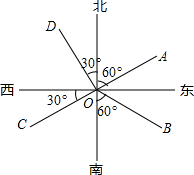 如图所示的四条射线中,表示北偏西30°的是( )
如图所示的四条射线中,表示北偏西30°的是( )
 如图所示的四条射线中,表示北偏西30°的是( )
如图所示的四条射线中,表示北偏西30°的是( )| A. | 射线OA | B. | 射线OB | C. | 射线OC | D. | 射线OD |
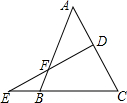 如图所示,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且$\frac{EF}{FD}$=$\frac{AC}{BC}$.求证:AD=EB.
如图所示,已知D为△ABC的边AC上的一点,E为CB的延长线上的一点,且$\frac{EF}{FD}$=$\frac{AC}{BC}$.求证:AD=EB. 如图,在?ABCD中,∠ABC的平分线交AD于点E,∠C=110°,BC=4cm,CD=3cm,则∠BED=145°,DE=1cm.
如图,在?ABCD中,∠ABC的平分线交AD于点E,∠C=110°,BC=4cm,CD=3cm,则∠BED=145°,DE=1cm.