题目内容
16. 如图,在?ABCD中,∠ABC的平分线交AD于点E,∠C=110°,BC=4cm,CD=3cm,则∠BED=145°,DE=1cm.
如图,在?ABCD中,∠ABC的平分线交AD于点E,∠C=110°,BC=4cm,CD=3cm,则∠BED=145°,DE=1cm.
分析 (1)根据平行四边形性质得出AD∥BC,∠ABC=∠D=70°,求出∠EBC的度数,根据平行线的性质得出∠BED+∠EBC=180°,代入求出即可;
(2)根据平行线性质和角平分线定义得出∠AEB=∠EBC=∠ABE,求出AB=AE=CD=3cm,代入AD-AE即可求出答案.
解答 解:(1)∵四边形ABCD是平行四边形,∠C=110°,
∴∠ABC=∠D=70°,AD∥BC,
∵BE平分∠ABC,∠ABC=70°,
∴∠EBC=35°,
∵AD∥BC,
∴∠EBC+∠BED=180°,
∴∠BED=145°,
故答案为:145°
(2)∵四边形ABCD是平行四边形,
∴AB=CD=3cm,AD=BC=4cm,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AE=AB=3cm,
∴DE=AD-AE=4cm-3cm=1cm.
故答案为:1cm.
点评 本题考查了等腰三角形的性质和判定,平行线性质,平行四边形性质等知识点,题目的综合性较强,难度中等,是一道不错的中考题,解题的关键是熟记平行四边形的各种性质.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
6.下列计算正确的是( )
| A. | 3ab-2ab=1 | B. | ($\sqrt{2}$+1)(1-$\sqrt{2}$)=1 | C. | -(-a)4÷a2=a2 | D. | $\root{3}{-8}$=-2 |
7.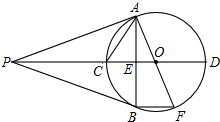 如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:
如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:
①∠ABP=∠AOP;②BC=DF; ③∠PAC=$\frac{1}{2}$∠AOP;④BE2=$\frac{PE•BF}{2}$
其中正确的结论有( )
 如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:
如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:①∠ABP=∠AOP;②BC=DF; ③∠PAC=$\frac{1}{2}$∠AOP;④BE2=$\frac{PE•BF}{2}$
其中正确的结论有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.如图图形中,阴影部分面积相等的是( )
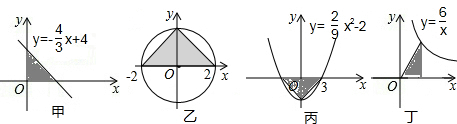

| A. | 甲乙 | B. | 甲丙 | C. | 乙丙 | D. | 丙丁 |
16. 如图,由B到A的方向是( )
如图,由B到A的方向是( )
 如图,由B到A的方向是( )
如图,由B到A的方向是( )| A. | 南偏东30° | B. | 东偏南60° | C. | 西偏北30° | D. | 北偏西60° |
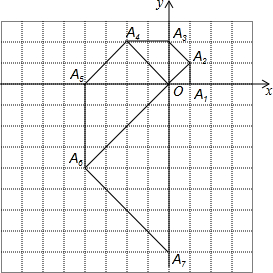 如图,O为坐标原点,点A1坐标为(1,0),以OA1为直角边作等腰直角△OA1A2,以OA2为直角边作等腰直角△OA2A3,以OA3为直角边作等腰直角△OA3A4,…,依此法继续作下去,OA2015=21007.
如图,O为坐标原点,点A1坐标为(1,0),以OA1为直角边作等腰直角△OA1A2,以OA2为直角边作等腰直角△OA2A3,以OA3为直角边作等腰直角△OA3A4,…,依此法继续作下去,OA2015=21007.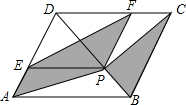 如图,菱形ABCD的边长为2,较短的对角线BD的长为3,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为$\frac{9}{4}$$\sqrt{3}$.
如图,菱形ABCD的边长为2,较短的对角线BD的长为3,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为$\frac{9}{4}$$\sqrt{3}$. 如图,在直线a、b、c、d构成的角中,已知∠1=∠3,∠2=110°,求∠4的度数.
如图,在直线a、b、c、d构成的角中,已知∠1=∠3,∠2=110°,求∠4的度数.