题目内容
2.(1)如图1,菱形ABCD中,∠BAD=120°,点E,F分别在边BC,CD上,∠EAF=60°,连接EF,作△AGF,使△AGF与△AEF关于直线AF对称,连接DG. 求证:DG=BE;(2)如图2,等腰△ABC中,∠BAC=120°,AB=AC,点M,N在边BC上,M在N的左边,且∠MAN=60°,若BM=2,NC=3,求MN的长.
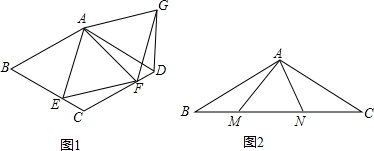
分析 (1)利用轴对称的性质可得∠GAF=∠EAF=60°,AG=AE,再得出∠BAE=∠DAG,从而证得△ABE≌△ADG,即可得出结论;
(2)作△APN,使△APN与△AMN关于直线AN对称,连接PC,由(1)可得△ABM≌△ACP,PC=BM=2,MN=PN,∠ACP=∠ABM=30°,进而得到∠NCP=60°,然后过点P作BC的垂线,垂足为E,利用勾股定理求解即可.
解答 (1)证明:∵△AGF与△AEF关于直线AF对称,
∴∠GAF=∠EAF=60°,AG=AE,
∵∠BAD=120°,
∴∠BAE+∠DAF=∠DAG+∠DAF=60°,
∴∠BAE=∠DAG,
∵四边形ABCD是菱形,
∴AB=AD,
在△ABE和△ADG中,
$\left\{\begin{array}{l}{AG=AE}\\{∠BAE=∠DAG}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADG,
∴DG=BE;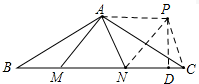 (2)解:作△APN,使△APN与△AMN关于直线AN对称,连接PC,
(2)解:作△APN,使△APN与△AMN关于直线AN对称,连接PC,
由(1)可得△ABM≌△ACP,PC=BM=2,MN=PN,∠ACP=∠ABM=30°,
∴∠NCP=60°,
过点P作BC的垂线,垂足为D,
∴CD=$\frac{1}{2}$PC=1,DN=CN-CD=2,
∴PD=PC•sin∠PCD=$\sqrt{3}$,
∴MN=PN=$\sqrt{P{D}^{2}+D{N}^{2}}$=$\sqrt{7}$.
点评 本题考查了菱形的性质,轴对称的性质,三角形的内角和定理,等腰三角形的性质,全等三角形的性质和判定的应用,解此题的关键是推出△ADC≌△BDF,注意:全等三角形的对应边相等,难度适中.

练习册系列答案
相关题目
13.已知边长为a的正方形面积为10,则下列关于a的说法中:
①a是无理数;②a是方程x2-10=0的解;③a是10的算术平方根; ④a满足不等式组$\left\{\begin{array}{l}{a-3>0}\\{a-4<0}\end{array}\right.$
正确的说法有( )
①a是无理数;②a是方程x2-10=0的解;③a是10的算术平方根; ④a满足不等式组$\left\{\begin{array}{l}{a-3>0}\\{a-4<0}\end{array}\right.$
正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.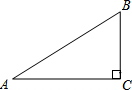 如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
 如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )
如图,已知在Rt△ABC中,∠C=90°,AC=4,tanA=$\frac{1}{2}$,则AB的长是( )| A. | 2 | B. | 8 | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
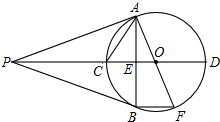 如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:
如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论: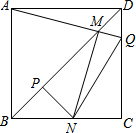 边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,有下列结论:
边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,有下列结论: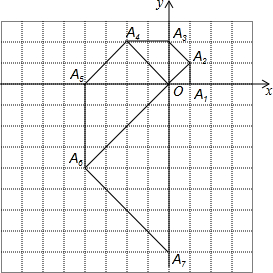 如图,O为坐标原点,点A1坐标为(1,0),以OA1为直角边作等腰直角△OA1A2,以OA2为直角边作等腰直角△OA2A3,以OA3为直角边作等腰直角△OA3A4,…,依此法继续作下去,OA2015=21007.
如图,O为坐标原点,点A1坐标为(1,0),以OA1为直角边作等腰直角△OA1A2,以OA2为直角边作等腰直角△OA2A3,以OA3为直角边作等腰直角△OA3A4,…,依此法继续作下去,OA2015=21007.