题目内容
13.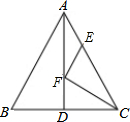 如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为$\frac{240}{13}$.
如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为$\frac{240}{13}$.
分析 作BE⊥AC垂足为E,交AD于F,此时CF+EF最小.
解答 解: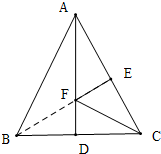 作BE⊥AC垂足为E,交AD于F,此时CF+EF最小.
作BE⊥AC垂足为E,交AD于F,此时CF+EF最小.
理由如下:∵AB=AC,AD是中线,
∴AD⊥BC,
∴FB=FC,
∴CF+EF=BF+EF,
∵线段BE是垂线段,根据垂线段最短,
∴点E、点F、就是所找的点.
∵$\frac{1}{2}$•BC•AD=$\frac{1}{2}$•AC•BE,
∴$\frac{1}{2}$×20×24=$\frac{1}{2}$×26×BE,
∴BE=$\frac{240}{13}$,
∴CF+EF的最小值=BE=$\frac{240}{13}$,
故答案为$\frac{240}{13}$.
点评 本题考查等腰三角形的性质、垂直平分线的性质、垂线段最短等知识,掌握应用面积法求高是解决这个问题的关键.

练习册系列答案
相关题目
18.扬州商场某商家计划购进一批甲、乙两种LED节能灯共120只,这两种节能灯的进价、售价如下表:
(1)如果进货总费用恰好为4600元,请你设计出进货方案.
(2)如果规定:当销售完这批节能灯后,总利润不超过进货总费用的30%,请问如何进货,使得该商家获得的总利润最多,此时总利润最多为多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)如果规定:当销售完这批节能灯后,总利润不超过进货总费用的30%,请问如何进货,使得该商家获得的总利润最多,此时总利润最多为多少元?
2.使分式$\frac{x+2}{{{x^2}+4}}$等于0的x值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 不存在 |
 如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125),以AB为直径的⊙M经过原点O.
如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125),以AB为直径的⊙M经过原点O.