题目内容
3. 如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125),以AB为直径的⊙M经过原点O.
如图,在直角坐标系中,抛物线与x轴交于A(1,0)、C两点(点C在点A的左侧),与y轴交于点B,且抛物线的顶点坐标为(-1.5,3.125),以AB为直径的⊙M经过原点O.(1)求抛物线的解析式;
(2)连接BC,判定BC与⊙M的位置关系,并说明理由;
(3)已知点P是抛物线上的一个动点,且在B、C两点之间,问当点P运动到什么位置时,△PBC的面积最大?并求出此时点P的坐标和△PBC的最大面积.
分析 (1)根据函数值相等的两点关于对称轴对称,可得C点坐标,根据待定系数法,可得函数解析式;
(2)根据相似三角形的判定与性质,可得∠1与∠3的关系,根据余角的性质,可得∠1与∠2的关系,根据切线的判定,可得答案;
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PD的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案.
解答 解:(1)由抛物线的顶点坐标为(-1.5,3.125),得
对称轴为x=-$\frac{3}{2}$.
由A、C关于对称轴对称,得
C点坐标是(-4,0).
设抛物线的解析式为y=ax2+bx+c,将A、B及顶点的坐标代入,得
$\left\{\begin{array}{l}{\frac{9}{4}a-\frac{3}{2}b+c=\frac{25}{8}}\\{16a-4b+c=0}\\{a+b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-\frac{3}{2}}\\{c=2}\end{array}\right.$,
抛物线的解析式为y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2;
(2)BC与⊙M相切,理由如下:
如图1: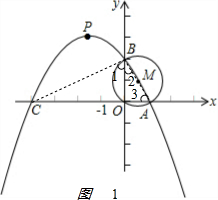 ,
,
$\frac{OC}{OB}$=$\frac{4}{2}$=2,$\frac{OB}{OA}$=$\frac{2}{1}$=2,
∴$\frac{OC}{OB}$=$\frac{OB}{OA}$,
∵∠BOC=∠AOB=90°,
∴△OBC∽△OAB,
∴∠1=∠3.
∵∠2+∠3=90°,
∴∠1+∠2=90°.
∴BC⊥BA.
∵BC经过半径的外端,
∴BC与⊙M相切.
(3)如图2: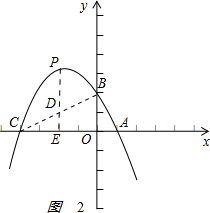 ,
,
BC的解析式为y=$\frac{1}{2}$x+2,设D(m,$\frac{1}{2}$m+2),P在抛物线上,设P(m,-$\frac{1}{2}$m2-$\frac{3}{2}$m+2).
PD的长为-$\frac{1}{2}$m2-$\frac{3}{2}$m+2-($\frac{1}{2}$m+2)=-$\frac{1}{2}$m2-2m=-$\frac{1}{2}$(m+2)2+2;
S△PBC=S△PDC+S△PDB
=$\frac{1}{2}$PD•CE+$\frac{1}{2}$PD•OE
=$\frac{1}{2}$PD•OC
=$\frac{1}{2}$×|-4|×[-$\frac{1}{2}$(m+2)2+2]
当m=-2时,S△PBC最大=4,
当m=-2时,-$\frac{1}{2}$m2-$\frac{3}{2}$m+2=3,即P(-2,3),
当P运动到(-2,3)时,S△PBC最大=4.
点评 本题考查了二次函数综合题,利用函数值相等的两点关于对称轴对称得出C点坐标是解题关键;利用相似三角形的判定与性质得出∠1与∠3的关系是解题关键,又利用了余角的性质,切线的判定;利用三角形的面积的和差得出二次函数是解题关键.

| A. | 打开电视机正在播放广告 | |
| B. | 投掷一枚质地均匀的硬币100次,正面向上的次数为50次 | |
| C. | 任意一个一元二次方程都有实数根 | |
| D. | 在平面上任意画一个三角形,其内角和是180° |
| A. | (-3,-5) | B. | (3,5) | C. | (3,-5) | D. | (5,-3) |
 如图,小明在大楼的东侧A处发现正前方仰角为75°的方向上有一热气球在C处,此时,小亮在大楼的西侧B处也测得气球在其正前方仰角为30°的位置上,已知AB的距离为60米,试求此时小明、小亮两人与气球的距离AC和BC.(结果保留根号)
如图,小明在大楼的东侧A处发现正前方仰角为75°的方向上有一热气球在C处,此时,小亮在大楼的西侧B处也测得气球在其正前方仰角为30°的位置上,已知AB的距离为60米,试求此时小明、小亮两人与气球的距离AC和BC.(结果保留根号)
 如图,在平面直角坐标系中xOy,二次函数y=ax2-2ax+3的图象与x轴分别交于点A、B,与y轴交于点C,AB=4,动点P从B点出发,沿x轴负方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线BC,垂足为Q.设P点移动的时间为t秒(t>0),△BPQ与△ABC重叠部分的面积为S.
如图,在平面直角坐标系中xOy,二次函数y=ax2-2ax+3的图象与x轴分别交于点A、B,与y轴交于点C,AB=4,动点P从B点出发,沿x轴负方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线BC,垂足为Q.设P点移动的时间为t秒(t>0),△BPQ与△ABC重叠部分的面积为S.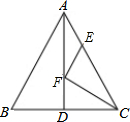 如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为$\frac{240}{13}$.
如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为$\frac{240}{13}$.