题目内容
1.$\sqrt{16}$的平方根是±2.函数y=$\sqrt{x-3}$中自变量x的取值范围是x≥3.分析 先计算$\sqrt{16}$,再求它的平方根即可,被开方数大于等于0,解不等式即可.
解答 解:∵$\sqrt{16}$=4,
∴4的平方根±2,
∵x-3≥0,
∴x≥3,
故答案为±2,x≥3.
点评 本题考查了函数自变量的取值范围问题以及平方根的求法,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.在平面直标坐标系中,点P(-3,-5)关于y轴对称点的坐标为( )
| A. | (-3,-5) | B. | (3,5) | C. | (3,-5) | D. | (5,-3) |
6.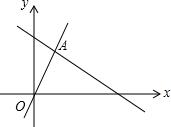 如图,函数y=2x和y=ax+2b的图象相交于点A(m,2),则不等式2x≤ax+2b的解集为( )
如图,函数y=2x和y=ax+2b的图象相交于点A(m,2),则不等式2x≤ax+2b的解集为( )
 如图,函数y=2x和y=ax+2b的图象相交于点A(m,2),则不等式2x≤ax+2b的解集为( )
如图,函数y=2x和y=ax+2b的图象相交于点A(m,2),则不等式2x≤ax+2b的解集为( )| A. | x<1 | B. | x>1 | C. | x≥1 | D. | x≤1 |
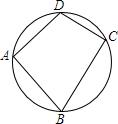 如图,点A、B、C、D在同一个圆上,若∠A=90°,CD=2,BC=3,这个圆的直径为$\sqrt{13}$.
如图,点A、B、C、D在同一个圆上,若∠A=90°,CD=2,BC=3,这个圆的直径为$\sqrt{13}$.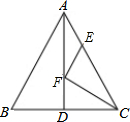 如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为$\frac{240}{13}$.
如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为$\frac{240}{13}$. 如图,有一块边长为a的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝行,再沿图中虚线折起,做成一个无盖的直三棱柱纸盒,若该纸盒侧面积的最大值是$\frac{9\sqrt{3}}{8}$cm2,则a的值为3cm.
如图,有一块边长为a的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝行,再沿图中虚线折起,做成一个无盖的直三棱柱纸盒,若该纸盒侧面积的最大值是$\frac{9\sqrt{3}}{8}$cm2,则a的值为3cm.