题目内容
5.计算:2cos45°-(-$\frac{1}{4}$)-1-$\sqrt{8}$-($\sqrt{2}$-π)0.分析 原式第一项利用特殊角的三角函数值计算,第二项利用负整数指数幂法则计算,第三项化为最简二次根式,最后一项利用零指数幂法则计算即可得到结果.
解答 解:原式=2×$\frac{\sqrt{2}}{2}$-(-4)-2$\sqrt{2}$-1=3-$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14.当x满足( )时,二次根式$\sqrt{1-x}$在实数范围内有意义.
| A. | x>1 | B. | x<1 | C. | x≤1 | D. | x≥1 |
15. 如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AD与FC分别是△ABC和△DEF的高,AC与DF交于点G,BC,DE在同一条直线上,则下列说法不正确的是( )
如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AD与FC分别是△ABC和△DEF的高,AC与DF交于点G,BC,DE在同一条直线上,则下列说法不正确的是( )
 如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AD与FC分别是△ABC和△DEF的高,AC与DF交于点G,BC,DE在同一条直线上,则下列说法不正确的是( )
如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AD与FC分别是△ABC和△DEF的高,AC与DF交于点G,BC,DE在同一条直线上,则下列说法不正确的是( )| A. | △AGD∽△CGF | B. | △AGD∽△DGC | C. | $\frac{{S}_{△AGD}}{{S}_{△CGF}}$=3 | D. | $\frac{AG}{CG}$=$\sqrt{3}$ |
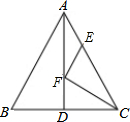 如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为$\frac{240}{13}$.
如图,△ABC中,AB=AC=26,BC=20,AD是BC边上的中线,AD=24,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为$\frac{240}{13}$. 目前,我市正积极推进“五城联创”,其中扩充改造绿地是推进工作计划之一.现有一块直角三角形绿地,量得两直角边长分别为a=9(米)和b=12(米),现要将此绿地扩充改造为等腰三角形,且扩充部分为含以b=12(米)为直角边的直角三角形,则扩充后等腰三角形的周长为40米或48米或(30+6$\sqrt{5}$)米.
目前,我市正积极推进“五城联创”,其中扩充改造绿地是推进工作计划之一.现有一块直角三角形绿地,量得两直角边长分别为a=9(米)和b=12(米),现要将此绿地扩充改造为等腰三角形,且扩充部分为含以b=12(米)为直角边的直角三角形,则扩充后等腰三角形的周长为40米或48米或(30+6$\sqrt{5}$)米.