题目内容
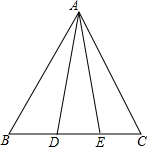 如图,在△ABC中,点D、E在边BC上,现有①AB=AC,②AD=AE,③BD=CE.请你用其中两个作为条件,余下一个作为结论,编写一道数学问题,并写出解答过程.
如图,在△ABC中,点D、E在边BC上,现有①AB=AC,②AD=AE,③BD=CE.请你用其中两个作为条件,余下一个作为结论,编写一道数学问题,并写出解答过程.已知:
求证:
证明:
考点:全等三角形的判定与性质
专题:
分析:由已知题设①AB=AC,②AD=AE,则得∠B=∠C,∠ADE=∠AED,所以得:∠ADB=∠AEC,即得△ABD≌△ACE,从而证得③BD=CE.
解答:已知AB=AC,AD=AE,
求证BD=CE.
证明:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
∴∠ADB=∠AEC,
在△ABD和△ACE中,
∴△ABD≌△ACE(AAS),
∴BD=CE.
故答案为AB=AC,AD=AE,BD=CE.
求证BD=CE.
证明:∵AB=AC,
∴∠B=∠C,
∵AD=AE,
∴∠ADE=∠AED,
∴∠ADB=∠AEC,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(AAS),
∴BD=CE.
故答案为AB=AC,AD=AE,BD=CE.
点评:此题考查的知识点是全等三角形的判定与性质,关键是由已知证△ABD≌△ACE.

练习册系列答案
相关题目
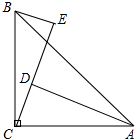 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为( )cm.
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为( )cm.| A、0.7 | B、1.7 |
| C、3.3 | D、2.3 |
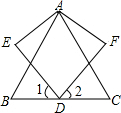 如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.
如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.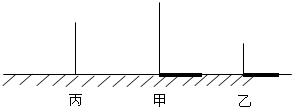 如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.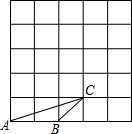 如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF,使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是
如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF,使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是