题目内容
 如图,△ABC为等边三角形,D为△ABC内的一点,且BD=DC,∠BDC=90°,已知AB=1,求AD的长.
如图,△ABC为等边三角形,D为△ABC内的一点,且BD=DC,∠BDC=90°,已知AB=1,求AD的长.考点:等边三角形的性质,等腰直角三角形
专题:
分析:延长AD交BC于点E,根据SSS定理可知△ABD≌△ACD,故∠BAD=∠CAD,所以AE是∠BAC的平分线,所以AE⊥BC,根据直角三角形的性质求出AE的长,由BD=DC,∠BDC=90°可得出DE的长,由AD=AE-DE即可得出结论.
解答: 解:延长AD交BC于点E,
解:延长AD交BC于点E,
在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AE是∠BAC的平分线,AE⊥BC.
∵等边△ABC的边长为1,
∴AE=AB•cos30°=1×
=
.
∵BD=DC,∠BDC=90°,
∴∠BAD=45°,
∴△BDE是等腰直角三角形,
∴DE=BE=
,
∴AD=AE-DE=
-
=
.
 解:延长AD交BC于点E,
解:延长AD交BC于点E,在△ABD与△ACD中,
|
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AE是∠BAC的平分线,AE⊥BC.
∵等边△ABC的边长为1,
∴AE=AB•cos30°=1×
| ||
| 2 |
| ||
| 2 |
∵BD=DC,∠BDC=90°,
∴∠BAD=45°,
∴△BDE是等腰直角三角形,
∴DE=BE=
| 1 |
| 2 |
∴AD=AE-DE=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查的是等边三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
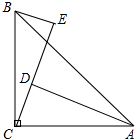 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为( )cm.
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,BE=0.8cm,则DE的长为( )cm.| A、0.7 | B、1.7 |
| C、3.3 | D、2.3 |
 如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.求证:
如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.求证: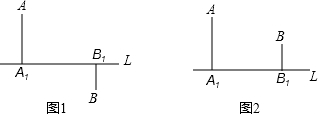
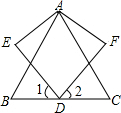 如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.
如图,△ABC中,AB=AC,D是BC的中点,∠AED=∠AFD=90°,AE=AF.