题目内容
8.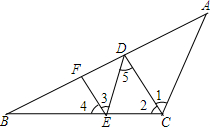 已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.
已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.证明:(请你在横线上填上合适的推理)
∵AC∥DE(已知),
∴∠1=∠5
同理∠5=∠3
∴∠1=∠3
∵DC∥EF(已知),
∴∠2=∠4
∵CD平分∠ACB,
∴∠1=∠2
∴∠3=∠4
∴EF平分∠BED.
分析 先根据平行线的性质得出∠BEF=∠BCD,∠FED=∠EDC,∠EDC=∠DCA,∠FED=∠DCA,故可得出∠FED=∠DCA,再根据CD平分∠ACB可知∠DCA=∠BCD,故可得出结论.
解答 证明:∵AC∥DE(已知)
∴∠1=∠5
同理∠5=∠3
∴∠1=∠3
∵DC∥EF(已知),
∴∠2=∠4
∵CD平分∠ACB,
∴∠1=∠2
∴∠3=∠4
∴EF平分∠BED.
故答案为:5,5,1,4,1,2,3,4.
点评 本题考查的是平行线的性质及角平分线的定义,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
5.若函数y=x2-2|x|+2-m的图象与x轴恰好有三个公共点,则实数m的值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
 如图是四张纸片拼成的图形,请利用图形面积的不同表示方式,写出一个a、b的恒等式.
如图是四张纸片拼成的图形,请利用图形面积的不同表示方式,写出一个a、b的恒等式. 如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )
如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=$\frac{y}{x}$.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )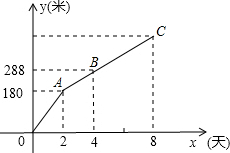 如图,是某工程队在“村村通”工程中修筑的公路长度y(米)与时间x(天)(其中0≤x≤8)之间的关系图象.根据图象提供的信息,求该公路的长.
如图,是某工程队在“村村通”工程中修筑的公路长度y(米)与时间x(天)(其中0≤x≤8)之间的关系图象.根据图象提供的信息,求该公路的长.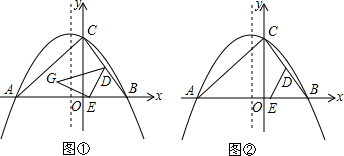
 如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6).那么:
如图所示,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动时间(0≤t≤6).那么: