题目内容
5.若函数y=x2-2|x|+2-m的图象与x轴恰好有三个公共点,则实数m的值是( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 把m=-2、-1、1、2分别代入函数解析式,分类讨论:当x≥0或x<0时得到二次函数解析式,然后根据抛物线与x轴的交点问题确定图象与x轴的公共点的个数.
解答 解:A、当m=-2时,y=x2-2|x|+4,当x≥0时,抛物线y=x2-2x+4与x轴没有公共点;当x<0时,抛物线y=x2+2x+4与x轴没有公共点,所以A选项错误;
B、当m=-1时,y=x2-2|x|+3,当x≥0时,抛物线y=x2-2x+3与x轴没有公共点;当x<0时,抛物线y=x2+2x+3与x轴没有公共点,所以B选项错误;
C、当m=1时,y=x2-2|x|+1,当x≥0时,抛物线y=x2-2x+1与x轴有1个公共点;当x<0时,抛物线y=x2+2x+1与x轴有1个公共点,所以C选项错误;
D、当m=2时,y=x2-2|x|,当x≥0时,抛物线y=x2-2x+与x轴的交点坐标为(0,0)、(2,0);当x<0时,抛物线y=x2+2x与x轴的交点坐标为(-2,0),所以D选项正确.
故选D.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标;二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了分类讨论的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.如果把$\frac{5xy}{x+y}$中的x与y都扩大为原来的10倍,那么这个代数式的值( )
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 扩大为原来的10倍 | D. | 缩小为原来的$\frac{1}{10}$ |
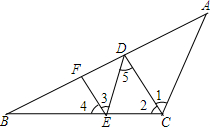 已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.
已知:如图,AC∥DE,DC∥EF,CD平分∠BCD.求证:EF平分∠BED.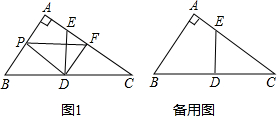
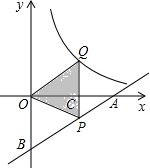 如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{5}{x}$(x>0)的图象于Q,则S△OQP=$\frac{7}{2}$.
如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{5}{x}$(x>0)的图象于Q,则S△OQP=$\frac{7}{2}$.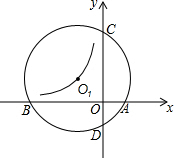 如图,⊙O1与坐标轴交于A、B、C、D四点,A(2,0)、B(-6,0)、D(0,-2),反比例函数y=$\frac{k}{x}$过O1,则k=-4.
如图,⊙O1与坐标轴交于A、B、C、D四点,A(2,0)、B(-6,0)、D(0,-2),反比例函数y=$\frac{k}{x}$过O1,则k=-4. 如图,矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,已知AB=3,AD=4,求△AEO的面积.
如图,矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,已知AB=3,AD=4,求△AEO的面积.