题目内容
3.化工公司销售某种新型化工原料,其市场指导价是每千克160元(化工公司的售价还可以在市场指导价的基础上进行浮动),这种原料的进货价是市场指导价的75%.(1)为了扩大销售量,化工公司决定适当调整价格,调整后的价格按八折销售,仍可获得20%的利润,求化工公司调整价格后的标价是多少元?
(2)经过市场调查发现,这种原料的日销售量y(千克)与实际售价x(元)之间的函数关系为y=-2x+400,当该公司售价为多少元时,每天的销售利润为3000元;
(3)在(2)的条件下,该公司决定每销售一千克原料就捐赠a元利润(a<10)给希望工程,公司通过销售记录发现,当售价在163元以内时,每天扣除捐赠后的日销售利润随时间(天)的增大而增大,直接写出a的取值范围.
分析 (1)根据题目可以求得进货价,由进货价可以求得调整后的价格,从而可以求得化工公司调整价格后的标价是多少元;
(2)根据利润等于售价减去成本然后再乘以销售量,即可解答本题;
(3)根据题意可以列出相应的关系式,根据最值问题可以解答本题.
解答 解:(1)由题意可得,进货价为:160×75%=120(元),
化工公司调整价格后的标价是:120×(1+20%)=144(元),
即化工公司调整价格后的标价是144元;
(2)由题意可得,
3000=(x-120)×(-2x+400)
解得,x1=150,x2=170
即该公司售价为150元或170元时,每天的销售利润为3000元;
(3)6<a<10.
设每天扣除捐赠后的日销售利润为b,
b=(x-120)×(-2x+400)-a(-2x+400)=(x-120-a)(-2x+400)=-2x2+(640+2a)x-(48000+400a),
∵当售价在163元以内时,每天扣除捐赠后的日销售利润随时间(天)的增大而增大,
∴$-\frac{640+2a}{2×(-2)}>163$
解得a>6,
又∵a<10,
∴6<a<10.
点评 本题考查二次函数的应用,解题的关键是根据题意可以列出相应的关系式,根据二次项系数可以判断二次函数的最值,并能求出这个最值.

练习册系列答案
相关题目
2.已知x=-1是方程2x+m-4=0的解,则m的值为( )
| A. | 6 | B. | 2 | C. | 0 | D. | -6 |
 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别在菱形的边BC、CD上运动,且∠EAF=60°且E、F不与B、C、D重合,连接AC交EF于P点.
如图所示,在菱形ABCD中,AB=4,∠BAD=120°,点E、F分别在菱形的边BC、CD上运动,且∠EAF=60°且E、F不与B、C、D重合,连接AC交EF于P点.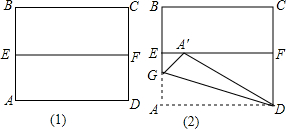 如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线DG折叠,使A点落在EF上,对应点为A′,求∠DA′F的度数.
如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线DG折叠,使A点落在EF上,对应点为A′,求∠DA′F的度数. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=15cm,则点D到AB的距离是15cm.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交BC于点D,CD=15cm,则点D到AB的距离是15cm.