题目内容
1.函数y=$\frac{2x-1}{\sqrt{3x-6}}$的自变量取值范围是x>2.分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:由题意,得
3x-6>0.
解得x>2,
故答案为:x>2.
点评 本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
11.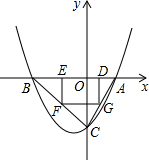 如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
(1)求抛物线表达式及A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并求出面积的最大值及m的取值范围.
 如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:| x | … | -3 | -2 | 1 | 2 | … |
| y | … | $-\frac{5}{2}$ | -4 | $-\frac{5}{2}$ | 0 | … |
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并求出面积的最大值及m的取值范围.
6.若方程组$\left\{\begin{array}{l}{x-2y=3}\\{3x+4y=5}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2.2}\\{y=-0.4}\end{array}\right.$,则方程组$\left\{\begin{array}{l}{(a+2012)-2(b-2013)=3}\\{3(a+2012)+4(b-2013)=5}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{a=2.2}\\{b=-0.4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=2014.2}\\{b=2012.6}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{a=-2009.8}\\{b=2012.6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2014.2}\\{b=2013.4}\end{array}\right.$ |
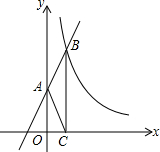 如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过点B作BC⊥x轴于点C,连接AC,若tan∠ACO=2,则此反比例函数解析式为y=$\frac{4}{x}$.
如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过点B作BC⊥x轴于点C,连接AC,若tan∠ACO=2,则此反比例函数解析式为y=$\frac{4}{x}$.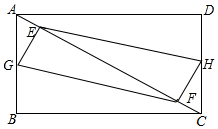 在矩形ABCD中,AB=3,BC=4,E,F是对角线ACS行的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动.
在矩形ABCD中,AB=3,BC=4,E,F是对角线ACS行的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动. 如图1,已知三角形纸片ABC,AB=AC,∠A=50°,将其折叠,如图2,使点A与点B重合,折痕为ED,点E、D分别在AB、AC上,则∠DBC=15°.
如图1,已知三角形纸片ABC,AB=AC,∠A=50°,将其折叠,如图2,使点A与点B重合,折痕为ED,点E、D分别在AB、AC上,则∠DBC=15°.